
【题目】如图,抛物线y=ax2 +bx+ 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
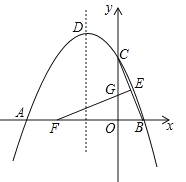
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
【答案】(1)![]() 顶点D的坐标为(-1,
顶点D的坐标为(-1,![]() )
)
(2)H(![]() ,
,![]() )
)
(3)K(-![]() ,
,![]() )
)
【解析】
(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值,进而可用配方法求出其顶点D的坐标;
(2)根据抛物线的解析式可求出C点的坐标,由于CD是定长,若△CDH的周长最小,那么CH+DH的值最小,由于EF垂直平分线段BC,那么B、C关于直线EF对称,所以BD与EF的交点即为所求的H点;易求得直线BC的解析式,关键是求出直线EF的解析式;由于E是BC的中点,根据B、C的坐标即可求出E点的坐标;可证△CEG∽△COB,根据相似三角形所得的比例线段即可求出CG、OG的长,由此可求出G点坐标,进而可用待定系数法求出直线EF的解析式,由此得解;
(3)过K作x轴的垂线,交直线EF于N;设出K点的横坐标,根据抛物线和直线EF的解析式,即可表示出K、N的纵坐标,也就能得到KN的长,以KN为底,F、E横坐标差的绝对值为高,可求出△KEF的面积,由此可得到关于△KEF的面积与K点横坐标的函数关系式,根据所得函数的性质即可求出其面积的最大值及对应的K点坐标.
(1)由题意,得![]() 解得
解得![]() ,b=-1.
,b=-1.
所以抛物线的解析式为![]() ,顶点D的坐标为(-1,
,顶点D的坐标为(-1,![]() ).
).
(2)设抛物线的对称轴与x轴交于点M.因为EF垂直平分BC,即C关于直线EG的对称点为B,连结BD交于EF于一点,则这一点为所求点H,使DH+CH最小,即最小为
DH+CH=DH+HB=BD=![]() .而
.而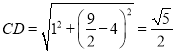 .
.
∴△CDH的周长最小值为CD+DR+CH=![]() .
.
设直线BD的解析式为y=k1x+b,则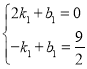 解得
解得![]() ,b1= 3.
,b1= 3.
所以直线BD的解析式为y=![]() x+ 3.
x+ 3.
由于BC= 2![]() ,CE=BC∕2 =
,CE=BC∕2 =![]() ,Rt△CEG∽△COB,
,Rt△CEG∽△COB,
得CE:CO=CG:CB,所以CG= 2.5,GO= 1.5.G(0,1.5).
同理可求得直线EF的解析式为y=![]() x+
x+![]() .
.
联立直线BD与EF的方程,解得使△CDH的周长最小的点H(![]() ,
,![]() ).
).
(3)设K(t,![]() ),xF<t<xE.过K作x轴的垂线交EF于N.
),xF<t<xE.过K作x轴的垂线交EF于N.
则KN=yK-yN=![]() -(
-(![]() t+
t+![]() )=
)=![]() .
.
所以S△EFK=S△KFN+S△KNE=![]() KN(t+ 3)+
KN(t+ 3)+![]() KN(1-t)= 2KN= -t2-3t+ 5 =-(t+
KN(1-t)= 2KN= -t2-3t+ 5 =-(t+![]() )2+
)2+![]() .
.
即当t=-![]() 时,△EFK的面积最大,最大面积为
时,△EFK的面积最大,最大面积为![]() ,此时K(-
,此时K(-![]() ,
,![]() ).
).


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图①,E在AB上,![]() 、
、![]() 都为等腰直角三角形,
都为等腰直角三角形,![]() ,连接DB,以DE、DB为边作平行四边形DBFE,连接FC、DC.
,连接DB,以DE、DB为边作平行四边形DBFE,连接FC、DC.
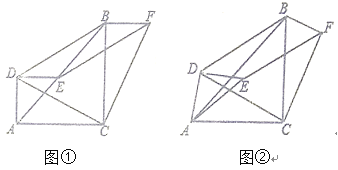
(1)求证:![]() ;
;![]() ;
;
(2)将图①中![]() 绕A点顺时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.
绕A点顺时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.
(3)将图①中的![]() 绕A点顺时针旋转
绕A点顺时针旋转![]() ,
,![]() ,其它条件不变,当四边形DBFE为矩形时,直接写出
,其它条件不变,当四边形DBFE为矩形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
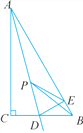
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=60°,D是BC边上的点,CD=1,将△ACD沿直线AD翻折,点C刚好落在AB边上的点E处.若P是直线AD上的动点,则△PEB的周长的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑球和白球,这些球除颜色外无其他差别,现让学生进行摸球试验:每次摸出一个球,记下颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 38 | 79 | 121 | 196 | 322 | 398 |
摸到黑棋的频率 | 0.380 | 0.395 | 0.403 | 0.392 | 0.403 | 0.398 |
(1)根据表中数据估计,从盒中摸出一个球是白球的概率是_____(精确到0.01);
(2)若盒中黑球与白球共有5枚,某同学连续不放回地摸出两个球,用树状图或表格计算这两个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
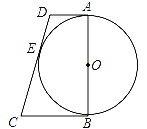
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
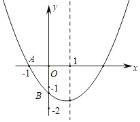
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和C(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2<8a;④![]() ;⑤b<c.其中含所有正确结论的选项是_____.
;⑤b<c.其中含所有正确结论的选项是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com