
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
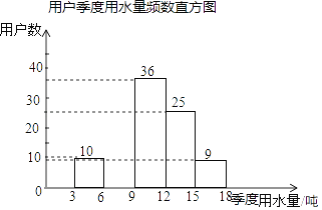
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=_______,n=________;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
【答案】(1)20;0.25;(2)补全频数直方图如图所示,见解析;(3)该社区用户中约有1500户家庭能够全部享受基本价格.
【解析】
(1)根据频率=频数÷数据总数,可得到m÷100=0.2,可求得m的值,然后利用频率=频数÷数据总数,可求得n的值;
(2)根据(1)中的计算结果,画出统计图即可;
(3)求得100户家庭中能够全部享受基本价的百分比,然后再乘5000,即可得到该社区用户中能够全部享受基本价格的家庭数量.
(1)20;0.25;
m÷100=0.2,
解得m=20,
n=25÷100=0.25;
故答案为:20;0.25;
(2)解:补全频数直方图如图所示:
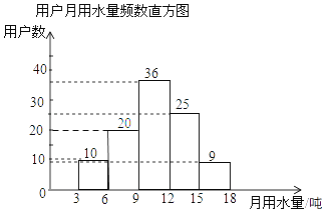
(3)(10+20)÷100×5000=1500(户).
答:该社区用户中约有1500户家庭能够全部享受基本价格.


科目:初中数学 来源: 题型:
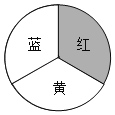
【题目】某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖(若指针恰好停在分割线上则重转).
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品.
(1)若选择方案一,则可领取一份奖品的概率是 ;
(2)选择哪个方案可以使领取一份奖品的可能性更大?请用列表法或画树状图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2015年市政府共投资3亿元人民币建设了廉租房12万平方米,2017年计划投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,问从2015到2017年这三年共建设了多少万平方米廉租房?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列数据是甲、乙、丙三人各10轮投篮的得分(每轮投篮10次,每次投中记1分):
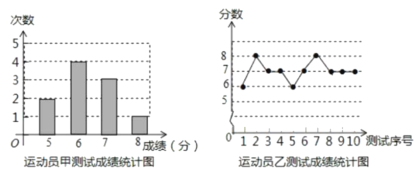
丙得分的平均数与众数都是7,得分统计表如下:
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
(1)丙得分表中的a= ,b= ;
(2)若在他们三人中选择一位投篮得分高且较为稳定的投手作为主力,你认为选谁更合适?请用你所学过的统计知识加以分析说明(参考数据:![]() ,
,![]() ,
,![]() );
);
(3)甲、乙、丙三人互相之间进行传球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,经过三次传球后球又回到乙手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。

(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
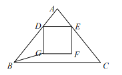
【题目】如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 上的两个动点(
上的两个动点(![]() 不与
不与![]() 重合),且保持
重合),且保持![]() ,以
,以![]() 为边,在点 A 的异侧作正方形
为边,在点 A 的异侧作正方形![]() .
.
(1)试求![]() 的面积;
的面积;
(2)当边![]() 与
与![]() 重合时,求正方形
重合时,求正方形![]() 的边长;
的边长;
(3)设![]() 与正方形
与正方形![]() 重叠部分的面积为
重叠部分的面积为![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的范围;
的范围;
(4)当![]() 是等腰三角形时,请直接写出
是等腰三角形时,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.
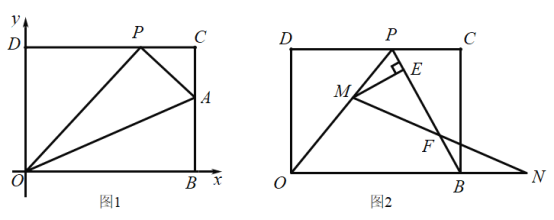
(1)若图1中的点 P 恰好是CD边的中点,求∠AOB的度数.
(2)如图1,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(3)如图2,在(2)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?
若变化,说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期三个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com