
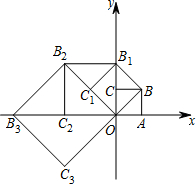
 如图,在平面直角坐标系中有一被称为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2020的坐标为(-21010,-21010).
如图,在平面直角坐标系中有一被称为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2020的坐标为(-21010,-21010). 分析 根据正方形的性质找出部分点Bn的坐标,由坐标的变化找出变化规律“B8n+1(0,24n+1),B8n+2(-24n+1,24n+1),B8n+3(-24n+2,0),B8n+4(-24n+2,-24n+2),B8n+5(0,-24n+3),B8n+6(24n+3,-24n+3),B8n+7(24n+4,0),B8n+8(24n+4,24n+4)”,依此规律即可得出结论.
解答 解:观察,发现规律:B1(0,2),B2(-2,2),B3(-4,0),B4(-4,-4),B5(0,-8),B6(8,-8),B7(16,0),B8(16,16),B9(0,32),
∴B8n+1(0,24n+1),B8n+2(-24n+1,24n+1),B8n+3(-24n+2,0),B8n+4(-24n+2,-24n+2),B8n+5(0,-24n+3),B8n+6(24n+3,-24n+3),B8n+7(24n+4,0),B8n+8(24n+4,24n+4).
∵2020=8×252+4,
∴B2020(-21010,-21010).
故答案为:(-21010,-21010).
点评 本题考查了规律型中的点的坐标的变化,解题的关键是找出点的变化规律“B8n+1(0,24n+1),B8n+2(-24n+1,24n+1),B8n+3(-24n+2,0),B8n+4(-24n+2,-24n+2),B8n+5(0,-24n+3),B8n+6(24n+3,-24n+3),B8n+7(24n+4,0),B8n+8(24n+4,24n+4)”.本题属于中档题,难度不大,解决该题型题目时,根据点的坐标变化找出变化规律是关键.


科目:初中数学 来源: 题型:填空题
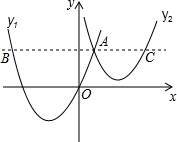 如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=$\frac{1}{2}$(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的中垂线.正确结论是①③④(填写正确结论的序号).
如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=$\frac{1}{2}$(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的中垂线.正确结论是①③④(填写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
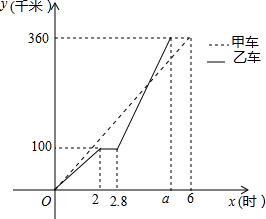 甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,
甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
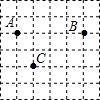 吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )
吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
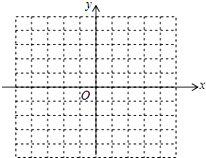 在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出将△ABC向右平移3个单位得到的△A1B1C1.
在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出将△ABC向右平移3个单位得到的△A1B1C1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com