
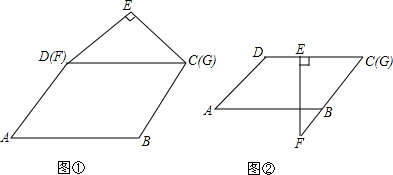
分析 根据平行四边形两邻角互补,∠ABC=3∠A,可得∠A=45°,再根据平行四边形的性质可得∠BCD的度数,根据重合可得Rt△EFG是等腰直角三角形,再根据等腰直角三角形的性质以及线段的和差关系即可得到DE有多长.
解答 解:∵四边形ABCD是平行四边形,
∴∠ABC+∠A=180°,∠A=∠BCD,
∵∠ABC=3∠A,
∴3∠A+∠A=180°,
∴∠A=45°,
∴∠BCD=45°,
∴∠EGF=45°,
∵∠FEG=90°,EF=2cm,
∴EG=2cm,CD=FG=2$\sqrt{2}$cm,
∴DE=2($\sqrt{2}$-1)cm.
故DE有2($\sqrt{2}$-1)cm长.
点评 考查了图形的剪拼,平行四边形的性质,等腰直角三角形的性质,本题关键是得到Rt△EFG是等腰直角三角形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
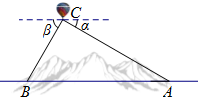 2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)
2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com