如图，公路上A、B两站相距25km，在公路AB附近有C、D两学校，DA⊥AB于点A，CB⊥AB于点B．已知DA=15km，CB=10km，现要在公路上建设一个青少年活动中心E，要使得C、D两学校到E的距离相等，则E应建在距A多远处？

分析：设AE=xkm，则BE=（25-x）km．根据勾股定理列出关于x的方程，通过解方程求得x，即AE的长度即可．

解答：解：设AE=xkm，则BE=（25-x）km；
由勾股定理，得
AE²+AD²=DE²，BE²+BC²=CE²，
则x²+15²=（25-x）²+10²，
解得x=10，
∴E应建在距A 10km处．

点评：本题考查了勾股定理的应用．根据勾股定理列出方程是此题的难点．

练习册系列答案

中考面对面系列答案

相关习题

科目：初中数学 来源： 题型：

如图①，一条笔直的公路上有A、B、C三地，B、C两地相距 150千米，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B两地．甲、乙两车到A 地的距离y₁、y₂（千米）与行驶时间x（时）的关系如图②所示．

根据图象进行以下探究：
（1）请在图①中标出 A地的位置，并作简要说明；
（2）甲的速度为

km/h，乙的速度为

km/h；
（3）求图②中M点的坐标，并解释该点的实际意义；
（4）在图②中补全甲车到达C地的函数图象，求甲车到A地的距离y₁与行驶时间x的函数关系式；
（5）出发多长时间，甲、乙两车距A点的距离相等？

科目：初中数学 来源：中华题王　数学　八年级上　(人教版) 人教版 题型：044

如图所示，公路上A、B两站(视为线上两点)相距25 km，C、D为公路同旁的两个村庄(视为两点)，DA⊥AB于A点，CB⊥AB于B点，DA＝15 km，CB＝10 km，现在要在公路AB上建一土特产品收购站E，使C、D两村庄到E站距离相等，则E站应建在距A站多少千米处？

科目：初中数学 来源：解题升级　　解题快速反应一典通　　九年级级数学 题型：044

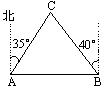
如图，公路上A、B两处相距1km，测得城镇C在A处的北偏东方向，在B处的北偏西方向，求城镇C到A处、B处的距离分别是多少？

科目：初中数学 来源： 题型：解答题

如图，公路上A、B两站相距25km，在公路AB附近有C、D两学校，DA⊥AB于点A，CB⊥AB于点B．已知DA=15km，CB=10km，现要在公路上建设一个青少年活动中心E，要使得C、D两学校到E的距离相等，则E应建在距A多远处？

同步练习册答案