
【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.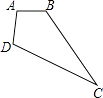
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.
【答案】
(1)解:相等.
理由:连接AC,
在△ACD和△ACB中,
 ,
,
∴△ACD≌△ACB,
∴∠B=∠D.

(2)解:设AD=x,BC=y,
当点C在点D右侧时, ![]() ,解得
,解得 ![]() ,
,
当点C在点D左侧时, ![]() 解得
解得 ![]() ,
,
此时AC=17,CD=5,AD=8,5+8<17,
∴不合题意,
∴AD=13cm,BC=10cm.
【解析】本题考查全等三角形的判定和性质、二元一次方程组、三角形三边关系定理等知识,解题的关键是学会分类讨论,考虑问题要全面,属于中考常考题型.(1)相等.连接AC,根据SSS证明两个三角形全等即可.(2)分两种情形①当点C在点D右侧时,②当点C在点D左侧时,分别列出方程组即可解决问题,注意最后理由三角形三边关系定理,检验是否符合题意.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
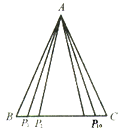
A. 4 B. 14 C. 40 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点坐标分别是
的顶点坐标分别是![]() 、
、![]() 、
、![]() .
.
![]() 如果将
如果将![]() 向上平移1个单位长度,再向左平移2个单位长度,得到
向上平移1个单位长度,再向左平移2个单位长度,得到![]() ,直接写出
,直接写出![]() 、
、![]() 的坐标,并求
的坐标,并求![]() 的面积;
的面积;
![]() 求出线段AB在
求出线段AB在![]() 中的平移过程中扫过的面积.
中的平移过程中扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )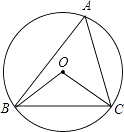
A.3 ![]()
B.4 ![]()
C.5 ![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现营养套餐的合理搭配,某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮.甲种袋装粗粮每袋含有3千克A粗粮,1千克B粗粮,1千克C粗粮;乙种袋装粗粮每袋含有1千克A粗粮,2千克B粗粮,2千克C粗粮.甲、乙两种袋装粗粮每袋成本分别等于袋中的A、B、C三种粗粮成本之和.已知每袋甲种粗粮的成本是每千克A种粗粮成本的7.5倍,每袋乙种粗粮售价比每袋甲种粗粮售价高20%,乙种袋装粗粮的销售利润率是20%.当销售这两款袋装粗粮的销售利润率为24%时,该电商销售甲、乙两种袋装粗粮的袋数之比是_____(商品的销售利润率=![]() ×100%)
×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年在中央“房子是用来住的,不是用来炒”的精神作用下,房子价格持续下跌.玲玲家买了一套新房准备装修,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费为4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑应选哪家公司?
(2)如果从节约开支的角度考虑应选哪家公司?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com