
分析 根据mapbq与-3ab2p+1的差为-$\frac{3}{2}$apbq,可以求得p、q的值,从而可以求得p+q的值.
解答 解:∵mapbq与-3ab2p+1的差为-$\frac{3}{2}$apbq,
∴$m{a}^{p}{b}^{q}-(-3a{b}^{2p+1})=-\frac{3}{2}{a}^{p}{b}^{q}$,
∴$m{a}^{p}{b}^{q}+3a{b}^{2p+1}=-\frac{3}{2}{a}^{p}{b}^{q}$,
∴$\left\{\begin{array}{l}{m+3=-\frac{3}{2}}\\{p=1}\\{q=2p+1}\end{array}\right.$
解得,$\left\{\begin{array}{l}{m=-\frac{9}{2}}\\{p=1}\\{q=3}\end{array}\right.$,
∴p+q=1+3=4.
点评 本题考查合并同类项,解题的关键是明确同类项的定义,会合并同类项.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:解答题
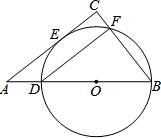 如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF.
如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
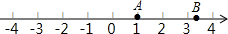 如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )| A. | -$\sqrt{10}$ | B. | -1-$\sqrt{10}$ | C. | $\sqrt{10}$-2 | D. | 2-$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com