
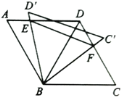
【题目】如图,![]() 中,
中,![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() 时,给出以下结论:①
时,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周长的最小值是
的周长的最小值是![]() .其中正确的是( )
.其中正确的是( )
A. ①②③B. ①②④C. ②③④D. ①③④
【答案】B
【解析】
根据题意可证△ABE≌△BDF,可判断①②③,由△DEF的周长=DE+DF+EF=AD+EF=4+EF,则当EF最小时△DEF的周长最小,根据垂线段最短,可得BE⊥AD时,BE最小,即EF最小,即可求此时△BDE周长最小值.
解:∵AB=BC=CD=AD=4,∠A=∠C=60°
∴△ABD,△BCD为等边三角形,
∴∠A=∠BDC=60°,
∵将△BCD绕点B旋转到△BC'D'位置,
∴∠ABD'=∠DBC',且AB=BD,∠A=∠DBC',
∴△ABE≌△BFD,
∴AE=DF,BE=BF,∠AEB=∠BFD,
∴∠BED+∠BFD=180°,
故①正确,③错误;
∵∠ABD=60°,∠ABE=∠DBF,
∴∠EBF=60°,
故②正确
∵△DEF的周长=DE+DF+EF=AD+EF=4+EF,
∴当EF最小时,∵△DEF的周长最小.
∵∠EBF=60°,BE=BF,
∴△BEF是等边三角形,
∴EF=BE,
∴当BE⊥AD时,BE长度最小,即EF长度最小,
∵AB=4,∠A=60°,BE⊥AD,
∴EB=![]() ,
,
∴△DEF的周长最小值为4+![]() ,
,
故④正确,
综上所述:①②④说法正确,
故选:B.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).
(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
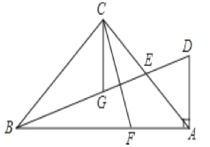
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
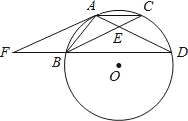
【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=![]() ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=![]() BD,连接AF.
BD,连接AF.
(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
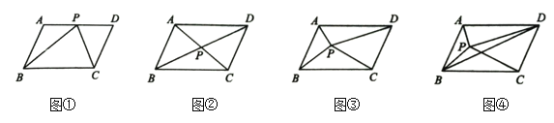
【题目】如图,四边形![]() 是面积为
是面积为![]() 的平行四边形,其中
的平行四边形,其中![]() .
.
(1)如图①,点![]() 为
为![]() 边上任意一点,则
边上任意一点,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)如图②,设![]() 交于点
交于点![]() ,则
,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是___________;
之间的数量关系是___________;
(3)如图③,点![]() 为
为![]() 内任意一点时,试猜想
内任意一点时,试猜想![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(4)如图④,已知点![]() 为
为![]() 内任意一点,
内任意一点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上![]() 点、
点、![]() 点表示的数分别为
点表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)
在数轴上,点![]() 表示的数为-20,点
表示的数为-20,点![]() 表示的数为10,动点
表示的数为10,动点![]() 从点
从点![]() 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点![]() 也从点
也从点![]() 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时,![]() 、
、![]() 两点相遇,且动点
两点相遇,且动点![]() 、
、![]() 运动的速度之比是
运动的速度之比是![]() (速度单位:单位长度/秒).
(速度单位:单位长度/秒).
![]()
![]()
备用图
(综合运用)
(1)点![]() 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点![]() 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;
(2)当![]() 时,求运动时间;
时,求运动时间;
(3)若点![]() 、
、![]() 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也随着运动.问点
也随着运动.问点![]() 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点![]() 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置—、二、三等奖和进步奖共四个奖项,赛后将八年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请报据图中的信息,解答下列问题:

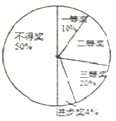
(1)八年级(1)班共有 名学生;
(2)将条形图补充完整;在扇形统计图中,“二等奖”对应的扇形的圆心角度数 ;
(3)如果该八年级共有800名学生,请估计荣获一、二、三等奖的学生共有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com