
 CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.
CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.分析 先依据线段垂直平分线的性质得到AC=BC,AD=BD,然后利用SSS证明△ADC≌△BDC.
解答 解:∵CD是线段AB的垂直平分线 (已知),
∴AC=BC,AD=BD(线段垂直平分线上的点到线段两端的距离相等)
在△ADC和△BDC中,
AC=BC,
AD=BD,
CD=CD( 公共边),
∴△ADC≌△BDC( SSS ).
∴∠CAD=∠CBD (全等三角形的对应角相等).
故答案为:BC;BC;线段垂直平分线上的点到线段两端的距离相等;△BDC;AC;BD;CD;公共边;△ADC;△BDC;SSS.
点评 本题主要考查的是全等三角形的性质和判定,线段垂直平分线的性质,熟练掌握相关性质是解题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=120°,则∠D=( )度.
如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=120°,则∠D=( )度.| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A类 | 100 | 30 |
| B类 | 200 | 25 |
| C类 | 500 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
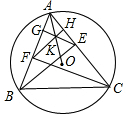 如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.
如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:| x(元) | 3 | 4 | 5 | 6 |
| y(个) | 20 | 15 | 12 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com