
【题目】如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(2,2),一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中,当△POA为等腰三角形时,请写出所有满足条件的点B的坐标__________.
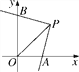
【答案】(0,2),(0,0),(0,4-2![]() )
)
【解析】由P坐标为(2,2),可得∠AOP=45°,然后分别从OA=PA,OP=PA,OA=OP去分析求解即可求得答案.
解:∵P坐标为(2,2),
∴∠AOP=45°,
①如图1,若OA=PA,则∠AOP=∠OPA=45°,
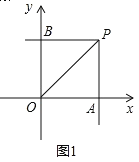
∴∠OAP=90°,
即PA⊥x轴,
∵∠APB=90°,
∴PB⊥y轴,
∴点B的坐标为:(0,2);
②如图2,若OP=PA,则∠AOP=∠OAP=45°,
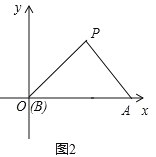
∴∠OPA=90°,
∵∠BPA=90°,
∴点B与点O重合,
∴点B的坐标为(0,0);
③如图3,若OA=OP,则∠OPA=∠OAP=![]() (180°∠AOP)=67.5°,
(180°∠AOP)=67.5°,
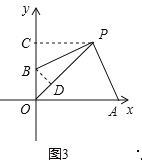
过点P作PC⊥y轴于点C,过点B作BD⊥OP于点D,
则PC∥OA,
∴∠OPC=∠AOP=45°,
∵∠APB=90°,
∴∠OPB=∠APB∠OPA=22.5°,
∴∠OPB=∠CPB=22.5°,
∴BC=BD,
设OB=a,
则BD=BC=2a,
∵∠BOP=45°,
在Rt△OBD中,BD=OBsin45°,
即2a=![]() a,
a,
解得:a=4-2![]() .
.
综上可得:点B的坐标为:(0,2),(0,0),(0, 4-2![]() ).
).
故答案为:(0,2),(0,0),(0, 4-2![]() ).
).


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.

(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明![]() ;
;
(2)若![]() ,G是EF的中点(如图2),直接写出∠BDG的度数;
,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若![]() ,FG∥CE,
,FG∥CE, ![]() ,分别连结DB、DG(如图3),求∠BDG的度数.
,分别连结DB、DG(如图3),求∠BDG的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从A出发,以每秒1cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD.
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B的路线运动,且在AB上以每秒1cm的速度匀速运动,(当P、Q中的某一点到达终点,则两点都停止运动.)过Q作直线QN,使QN∥PM,设点Q运动的时间为t秒(0≤t≤8),直线PM与QN截□ABCD所得图形的面积为S(cm2).求S关于t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线l经过A、C两点.
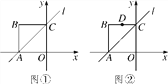
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;
(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.
①请求出|BE+DE|的最小值和此时点E的坐标;
②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|的最大值,并写出此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.
,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),如图
三个顶点都在小正方形的顶点处),如图![]() 所示.这样不需求
所示.这样不需求![]() 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.
(1)请你将![]() 的面积直接填写在横线上.__________________
的面积直接填写在横线上.__________________
思维拓展:
(2)我们把上述求![]() 面积的方法叫做构图法.若
面积的方法叫做构图法.若![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() (
(![]() ),请利用图
),请利用图![]() 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积.
,并求出它的面积.
探索创新:
(3)若![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() (
(![]() ,且
,且![]() ),试运用构图法求出这三角形的面积.(请用2B铅笔将所作图形加黑加粗)
),试运用构图法求出这三角形的面积.(请用2B铅笔将所作图形加黑加粗)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.

如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知)
且∠1=∠CGD(_______)
∴∠2=∠CGD(等量代换)
∴CE∥BF(_______)
∴∠_____=∠BFD(_______)
又∵∠B=∠C(已知)
∴∠BFD=∠B(_______)
∴AB∥CD(_______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com