
【题目】阅读下面内容,并解答问题:
杨辉和他的一个数学问题

我国古代对代数的研究,特别是对方程的解法研究有着优良的传统并取得了重要成果.
杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述,他著名的数学书共五种二十一卷,它们是:《详解九章算法》12卷(1261年),《日用算法》2卷(1262年),《乘除通变本末》3卷(1274年,第3卷与他人合编),《田(杨辉,南宋数学家)亩比类乘除捷法》2卷(1275年),《续古摘奇算法》2卷(1275年,与他人合编),其中后三种为杨辉后期所著,一般称之为《杨辉算法》.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除捷法》):
直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.
请你用学过的知识解决这个问题.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为( )

A.2B.4C.5﹣![]() D.8﹣2
D.8﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)若点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 与
与![]() 的数量关系是 ;线段
的数量关系是 ;线段![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
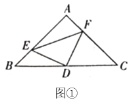
(2)如图①,若点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,上述结论是否依然成立,若成立,请证明;若不成立,请说明理由;
,上述结论是否依然成立,若成立,请证明;若不成立,请说明理由;
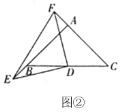
(3)如图②,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() ,直接写出
,直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,智能产品越来越受到人们的喜爱,为了奖励员工,某公司打算采购一批智能音箱.现有A,B两款智能音箱可供选择,已知A款音箱的单价比B款音箱的单价高50元,购买5个A款音箱和4个B款音箱共需1600元.
(1)分别求出A款音箱和B款音箱的单价;
(2)公司打算采购A,B两款音箱共20个,且采购A,B两款音箱的总费用不超过3500元,那么A款音箱最多采购多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
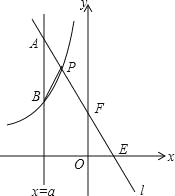
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=![]() (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
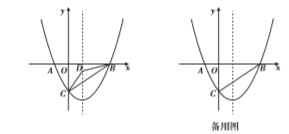
(1)求点![]() 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知点![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,
,![]() ,
,![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,设它们的运动时间为t秒.
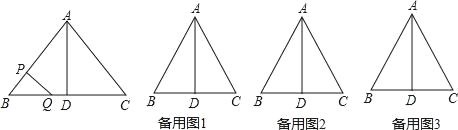
(1)若a=2,那么t为何值时△BPQ与△BDA相似?
(2)已知M为AC上一点,若当t=![]() 时,四边形PQCM是平行四边形,求这时点P的运动速度.
时,四边形PQCM是平行四边形,求这时点P的运动速度.
(3)在P、Q两点运动过程中,要使线段PQ在某一时刻平分△ABD的面积,点P的运动速度应限制在什么范围内?(提示:对于一元二次方程,有如下的结论:若x1x2是方程ax2+bx+c=0(a≠0)的两个根,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA=_____cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com