
ЁОЬтФПЁПФГЪ§бЇЪЕбщаЁзщдкЬНОПЁАЙигкxЕФЖўДЮШ§ЯюЪНax2+bx+3ЕФаджЪЃЈaЁЂbЮЊГЃЪ§ЃЉЁБЪБЃЌНјааСЫШчЯТЛюЖЏЃЎ
ЃЈЪЕбщВйзїЃЉШЁВЛЭЌЕФxЕФжЕЃЌМЦЫуДњЪ§ЪНax2+bx+3ЕФжЕЃЎ
x | Ё | Љ1 | 0 | 1 | 2 | 3 | Ё |
ax2+bx+3 | Ё | 0 | 3 | 4 | Ё |
ЃЈ1ЃЉИљОнЩЯБэЃЌМЦЫуГіaЁЂbЕФжЕЃЌВЂВЙГфЭъећБэИёЃЎЃЈЙлВьВТЯыЃЉЪЕбщаЁзщзщдБЃЌЙлВьБэИёЃЌЬсГівдЯТВТЯыЃЎЭЌбЇМзЫЕЃКЁАДњЪ§ЪНax2+bx+3ЕФжЕЫцзХxЕФдіДѓЖјдіДѓЁБЃЎЭЌбЇввЫЕЃКЁАВЛТлxШЁКЮжЕЃЌДњЪ§ЪНax2+bx+3ЕФжЕвЛЖЈВЛДѓгк4ЁБЃЎЁ
ЃЈ2ЃЉЧыФувВЬсГівЛИіКЯРэЕФВТЯыЃКЁЁ ЁЁЃЈбщжЄВТЯыЃЉЮвУЧжЊЕРЃЌВТЯыгаПЩФмЪЧе§ШЗЕФЃЌвВПЩФмЪЧДэЮѓЕФЃЎ
ЃЈ3ЃЉЧыФуЗжБ№ХаЖЯМзЁЂввСНЮЛЭЌбЇЕФВТЯыЪЧЗёе§ШЗЃЌШєВЛе§ШЗЃЌЧыОйГіЗДР§ЃЛШєе§ШЗЃЌЧыМгвдЫЕРэЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3ЃЌ0ЃЛЃЈ2ЃЉЕБxЃНЉ2КЭxЃН4ЪБЃЌДњЪ§ЪНЃЈax2+bx+3ЃЉЕФжЕЪЧЯрЕШЕФЃЛЃЈ3ЃЉМзЕФЫЕЗЈВЛе§ШЗЃЌЗДР§МћНтЮіЃЌввЕФЫЕЗЈе§ШЗЃЌМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§НтЗНГЬзщЧѓЕУaЁЂbЕФжЕЃЎ
ЃЈ2ЃЉПЩвдИљОнЖўДЮКЏЪ§yЃНax2+bx+3ЕФЭМЯѓаджЪНјааВТЯыЃЛ
ЃЈ3ЃЉОйГіЗДР§МДПЩХаЖЯЃЎ
НтЃКЃЈ1ЃЉЕБxЃНЉ1ЪБЃЌaЉb+3ЃН0ЃЛ
ЕБxЃН1ЪБЃЌa+b+3ЃН4ЃЎ
ПЩЕУЗНГЬзщ![]() ЃЎ
ЃЎ
НтЕУЃК![]() ЃЎ
ЃЎ
ЕБxЃН2ЪБЃЌax2+bx+3ЃН3ЃЛ
ЕБxЃН3ЪБЃЌax2+bx+3ЃН0ЃЎ
ЙЪД№АИЪЧЃК3ЃЛ0ЃЛ
ЃЈ2ЃЉбджЎгаРэМДПЩЃЌБШШчЕБxЃМ1ЪБЃЌЃЈax2+bx+3ЃЉЫцxЕФдіДѓЖјдіДѓЃЛЕБxЃНЉ2КЭxЃН4ЪБЃЌДњЪ§ЪНЃЈax2+bx+3ЃЉЕФжЕЪЧЯрЕШЕФЃЛ
ЙЪД№АИЪЧЃКЕБxЃНЉ2КЭxЃН4ЪБЃЌДњЪ§ЪНЃЈax2+bx+3ЃЉЕФжЕЪЧЯрЕШЕФЃЈД№АИВЛЮЈвЛЃЉЃЛ
ЃЈ3ЃЉМзЕФЫЕЗЈВЛе§ШЗЃЎ
ОйЗДР§ЃКЕБxЃН1ЪБЃЌyЃН4ЃЛЕЋЕБxЃН2ЪБЃЌyЃН3ЃЌЫљвдyЫцxЕФдіДѓЖјдіДѓЃЌетИіЫЕЗЈВЛе§ШЗЃЎ
ввЕФЫЕЗЈе§ШЗЃЎ
жЄУїЃКЉx2+2x+3ЃНЉЃЈxЉ1ЃЉ2+4ЃЎ
ЁпЃЈxЉ1ЃЉ2Ён0ЃЎ
ЁрЉЃЈxЉ1ЃЉ2+4Ём4ЃЎ
ЁрВЛТлxШЁКЮжЕЃЌДњЪ§ЪНax2+bx+3ЕФжЕвЛЖЈВЛДѓгк4ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдкЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌЕуEдкACЩЯЃЈЧвВЛгыЕуAЃЌCжиКЯЃЉЃЌдкЁїABCЕФЭтВПзїЁїCEDЃЌЪЙЁЯCED=90ЁуЃЌDE=CEЃЌСЌНгADЃЌЗжБ№вдABЃЌADЮЊСкБпзїЦНааЫФБпаЮABFDЃЌСЌНгAFЃЎ
ЃЈ1ЃЉЧыжБНгаДГіЯпЖЮAFЃЌAEЕФЪ§СПЙиЯЕ ЃЛ
ЃЈ2ЃЉНЋЁїCEDШЦЕуCФцЪБеыа§зЊЃЌЕБЕуEдкЯпЖЮBCЩЯЪБЃЌШчЭМЂкЃЌСЌНгAEЃЌЧыХаЖЯЯпЖЮAFЃЌAEЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉдкЭМЂкЕФЛљДЁЩЯЃЌНЋЁїCEDШЦЕуCМЬајФцЪБеыа§зЊЃЌЧыХаЖЯЃЈ2ЃЉЮЪжаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌНсКЯЭМЂлаДГіжЄУїЙ§ГЬЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌAB=10ЃЌBC=13ЃЌCD=12ЃЌAD=5ЃЌADЁЭCDЃЌЧѓЫФБпаЮABCDЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
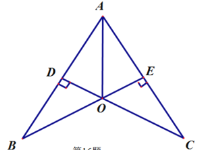
ЁОЬтФПЁПШчЭМЃЌвбжЊCDЁЭABгкЕуDЃЌBEЁЭ ACгкЕуEЃЌ CDЁЂ BEНЛгкЕуOЃЌЧвAOЦНЗжЁЯBACЃЌдђЭМжаЕФШЋЕШШ§НЧаЮЙВга_________________ЖдЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1дкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкЕуDЃЌBEЁЭMNгкЕуEЃЎ
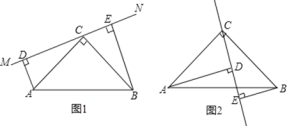
ЃЈ1ЃЉЧѓжЄЃКЂйЁїADCЁеЁїCEBЃЛЂкDE=AD+BEЃЎ
ЃЈ2ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМ2ЕФЮЛжУЪБЃЌDEЁЂADЁЂBEгждѕбљЕФЙиЯЕЃПВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛСОЛѕГЕДгГЌЪаГіЗЂЃЌЯђЖЋзпСЫ 3 ЧЇУзЕНДяаЁБђМвЃЌМЬајзп 2.5 УзЕНДяаЁгБМвЃЌШЛКѓЯђЮїзпСЫ 10 ЧЇУзЕНДяаЁУїМвЃЌзюКѓЛи ЕНГЌЪаЃЎ
ЃЈ1ЃЉаЁУїМвОраЁБђМвЖрдЖЃП
ЃЈ2ЃЉЛѕГЕвЛЙВааЪЛСЫЖрЩйЧЇУзЃП
ЃЈ3ЃЉЛѕГЕУПЧЇУзКФгЭ 0.2 Щ§ЃЌетДЮЙВКФгЭЖрЩйЩ§ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
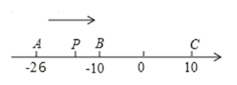
ЁОЬтФПЁПвбжЊЪ§жсЩЯга AЁЂBЁЂC Ш§ЕуЃЌЗжБ№БэЪОгаРэЪ§Ѓ26ЃЌЃ10ЃЌ10ЃЌЖЏЕу P Дг A ГіЗЂЃЌвдУПУы 1 Иі ЕЅЮЛЕФЫйЖШЯђжеЕу C вЦЖЏЃЌЩшЕу P вЦЖЏЪБМфЮЊ t УыЃЎ
ЃЈ1ЃЉгУКЌ t ЕФДњЪ§ЪНБэЪО P ЕНЕу A КЭЕуC ЕФОрРыЃКPA= ЃЌPC=
ЃЈ2ЃЉЕБЕу P дЫЖЏЕН B ЕуЪБЃЌЕу Q Дг A ЕуГіЗЂЃЌвдУПУы 3 ИіЕЅЮЛЕФЫй ЖШЯђ C ЕудЫЖЏЃЌQ ЕуЕНДя C ЕуКѓЃЌдйСЂМДвдЭЌбљЕФЫйЖШЗЕЛиЃЌЕБЕу P дЫЖЏЕНЕу C ЪБЃЌPЁЂQ СНЕудЫЖЏЭЃжЙЃЌ
ЂйЕБ PЁЂQ СНЕудЫЖЏЭЃжЙЪБЃЌЧѓЕу P КЭЕу Q ЕФОрРыЃЛ
ЂкЧѓЕБ t ЮЊКЮжЕЪБ PЁЂQ СНЕуЧЁКУдкЭОжаЯргіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAEЁЭBCгкEЃЌAFЁЭCDгкFЃЎ
ЃЈ1ЃЉЕуAЕНжБЯпBCЕФОрРыЪЧЯпЖЮ_______ЕФГЄЃЛ
ЃЈ2ЃЉЕуDЕНжБЯпAFЕФОрРыЪЧЯпЖЮ_______ЕФГЄЃЛ
ЃЈ3ЃЉЯпЖЮAFЕФГЄБэЪОЕуAЕНжБЯп_______ОрРыЃЛ
ЃЈ4ЃЉЯпЖЮCEЕФГЄБэЪОЕуCЕНжБЯп_______ОрРыЃЛ
ЃЈ5ЃЉЯпЖЮBEЕФГЄБэЪОЕу_______ЕНжБЯп______ОрРыЃЛ
ЃЈ6ЃЉЯпЖЮCFЕФГЄБэЪОЕу_______ЕНжБЯп______ОрРыЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,вбжЊABЁЮCD,ЕуEЁЂFЗжБ№дкжБЯпABЁЂCDЩЯ,ЁЯEPF=90ЁуЃЌЁЯBEP=ЁЯGEPЃЌдђЁЯ1гыЁЯ2ЕФЪ§СПЙиЯЕЮЊ( )

A. ЁЯ1=ЁЯ2B. ЁЯ1=2ЁЯ2C. ЁЯ1=3ЁЯ2D. ЁЯ1=4ЁЯ2
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com