
 ,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;
,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;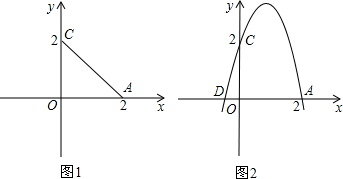
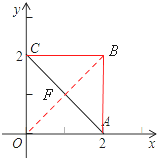 解:(1)设A的中点为F,连接OF并延长至B,使得BF=OF;
解:(1)设A的中点为F,连接OF并延长至B,使得BF=OF; ,0),
,0),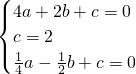 ,解得:
,解得: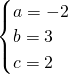 ,…
,… ,
, ,2).
,2). CE•AB=
CE•AB= ×
× ×2=
×2= .
. +b1=2,∴b1=
+b1=2,∴b1= ,∴y=-x+
,∴y=-x+ .
.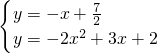 得:
得: 或
或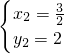 ∴点P1(
∴点P1( ,3).
,3). ),过点E′作直线n∥AC,与抛物线的交点为所求点P.与①同理,可求得直线n的表达式为y=-x+
),过点E′作直线n∥AC,与抛物线的交点为所求点P.与①同理,可求得直线n的表达式为y=-x+ ,则由
,则由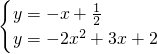 得:
得: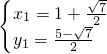 或
或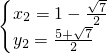 ,
, ,
,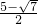 ),P3(1-
),P3(1- ,
,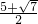 ).
).

科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |

查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北省武汉市青山区七年级第一学期期末测试数学试卷(带解析) 题型:解答题
如图l,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m-420|+(2n-40)2=0,射线OP从OB处绕点0以4度/秒的速度逆时针旋转.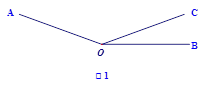
(1)试求∠AOB的度数;
(2)如图l,当射线OP从OB处绕点O开始逆时针旋转,同时射线OQ从OA处以l度/秒的速度绕点0顺时针旋转,当他们旋转多少秒时,使得∠POQ=10°?
(3)如图2,若射线OD为∠AOC的平分线,当射线OP从OB处绕点O开始逆时针旋转,同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转,使得这两条射线重合于射线OE处(OE在∠DOC的内部)时,且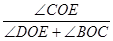 =
=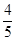 ,试求x.
,试求x.
查看答案和解析>>
科目:初中数学 来源:2015届湖北省武汉市青山区七年级第一学期期末测试数学试卷(解析版) 题型:解答题
如图l,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m-420|+(2n-40)2=0,射线OP从OB处绕点0以4度/秒的速度逆时针旋转.
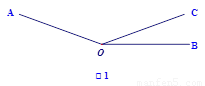
(1)试求∠AOB的度数;
(2)如图l,当射线OP从OB处绕点O开始逆时针旋转,同时射线OQ从OA处以l度/秒的速度绕点0顺时针旋转,当他们旋转多少秒时,使得∠POQ=10°?
(3)如图2,若射线OD为∠AOC的平分线,当射线OP从OB处绕点O开始逆时针旋转,同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转,使得这两条射线重合于射线OE处(OE在∠DOC的内部)时,且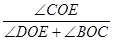 =
=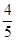 ,试求x.
,试求x.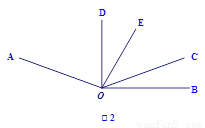
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
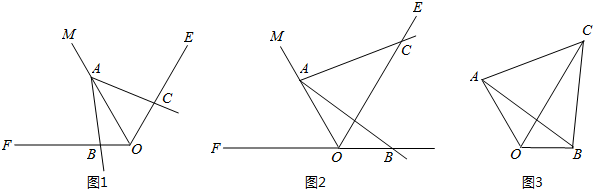
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com