
 如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:
如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:分析 (1)作相等的角,在角的边上截取相等的线段,找到对应点,顺次连接得出旋转后的图形.
(2)关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
解答 解:(1)如图所示,四边形A1B1C1D1、A2B2C2D2即为所求;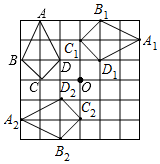
(2)∵A1A2,B1B2,C1C2,D1D2都经过点O,并且被点O平分,
∴四边形A1B1C1D1与四边形A2B2C2D2关于点O成中心对称.
故答案为:中心.
点评 本题主要考查了利用旋转变换进行作图以及中心对称的定义,解题时注意:把一个图形绕着某个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
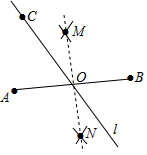 数学课上,老师提出如下问题:已知点A,B,C是不在同一直线上三点,求作一条过点C的直线l,使得点A,B到直线l的距离相等.
数学课上,老师提出如下问题:已知点A,B,C是不在同一直线上三点,求作一条过点C的直线l,使得点A,B到直线l的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).
如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
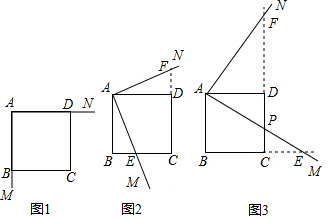
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).
已知,如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com