
����Ŀ����֪��ͼ���� ABC �У�BAC 90�� ,�ֱ������ B��C �� A ���ֱ�ߵĴ��ߴ���ֱ�Ϊ D��E,��̽���߶� BD��CE��DE ֮��Ĺ�ϵ.
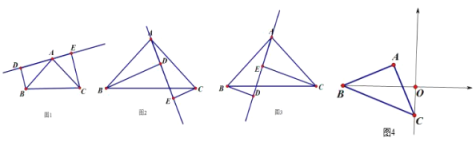
(1)��ֱ�� DE �Ƶ� A ��ת����ͼ 1 ��λ�ã�ֱ��д�� BD��CE��DE ֮������� Ϊ ��
(2)��ֱ�� DE �Ƶ� A ��ת����ͼ 2 ��λ�ã�ֱ��д�� BD��CE��DE ֮������� Ϊ ��
(3)��ֱ�� DE �Ƶ� A ��ת����ͼ 3 ��λ�ã�д�� BD��CE��DE ֮�����������֤�� ��Ľ��ۣ�
(4)��ͼ 4������� ABC ����ֱ������ϵ�У����� A ������Ϊ(-1,1),�� OB-OC �� ֵ.��д����Ҫ�Ľ����.
���𰸡���1��DE=BD+CE����2��DE=BD-CE����3��DE=CE-BD��֤������������4��2
��������
��1���� ADB=�� AEC=90����ת���õ��� DBA=�� EAC��֤���� DAB�ա� ECA�����ɵó��߶� BD��CE��DE ֮��Ĺ�ϵ����2����3��ͬ����֤�� DAB�ա� ECA�������BD��CE��DE ֮��Ĺ�ϵ����4����AD��ֱ��y���ڵ�D����AE��ֱ��x���ڵ�E��A������Ϊ��-1,1�������ı���AEODΪ�����Σ�֤���� BAE�ա� CAD���������OB-OC��ֵ
��1����BD�� DE��CE�� DE��
���� ADB=�� AEC=90����
���� BAC=90����
���� DAB+�� EAC=90������ DAB+�� DBA=90�㣬
��� DBA=�� EAC��
���� DAB���� ECA��

���� DAB�ա� ECA��AAS��
��DB=EA��DA=EC��
�� DE=BD+CE��
��2������ BAC=90����
���DAB+��EAC=90������DAB+��DBA=90�㣬
���DBA=��EAC��
���� DAB���� ECA��

���DAB�ա�ECA��AAS��
��DB=EA��DA=EC��
�� DE=BD-CE��
��3������ BAC=90����
���DAB+��EAC=90������DAB+��DBA=90�㣬
���DBA=��EAC��
���� DAB���� ECA��

���DAB�ա�ECA��AAS��
��DB=EA��DA=EC��
�� DE=CE-BD��
��4����ͼ����AD��ֱ��y���ڵ�D����AE��ֱ��x���ڵ�E��
��A��������-1,1����
���ADC=��AEO=90����AE=AD=1��
���ı���AEODΪ�����Σ�
���� EAD=90����
���EAC+�� DAC=90������ EAC+�� BAE=90����
��� BAE=�� CAD��
���� BAE���� CAD��

���� BAE �ա� CAD��AAS��
��BE=DC��
��OB=OE+BE��OC=CD-OD��
��OB-OC=��OE+EB��-��CD-OD��=OE+OD=2




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����֯���꼶160��ѧ���μ����ʵ���������35����45�����ֿͳ���������ÿ�ֿͳ�������1����������������
��1���μӱ��λ�����輸��45���ͳ�?
��2�����35���ͳ������Ϊÿ��300Ԫ��45���ͳ������Ϊÿ��400Ԫ��Ҫ��ʹȫ����ķ��ò�����1550Ԫ�����м�����ķ��������ַ�����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����OD��ֱ����AC�ڵ�E���ҽ���O�ڵ�D��F��BA�ӳ�����һ�㣬����CDB=��BFD��
��1����֤��FD�ǡ�O��һ�����ߣ�
��2����AB=10��AC=8����DF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ſƼ��뾭�õķ�չ���й������Ͷ��������ƿ�ʼ����ʧ������Ϊ��������Ļ����˲�ҵ��Ѹ�����𣬻������Զ����ߵ��г�ҲԽ��Խ������Ϊ�Զ��������ߵ���Ҫ��ʽ��ij������Ҫ�ڹ涨ʱ���ڰ���1200ǧԪ����ԭ�ϣ�����A��B���ֻ����˿ɹ�ѡ����֪A�ͻ����˱�B�ͻ�����ÿСʱ�����30ǧ�ˣ�A�ͻ����˰���900ǧ�����õ�ʱ����B�ͻ����˰���600ǧ�����õ�ʱ����ȣ�


��1�����ֻ�����ÿСʱ�ֱ���˶��ٻ���ԭ�ϣ�
��2���ù���ԭ�ƻ�ͬʱʹ�������ֻ����˰��ˣ�����һ��ʱ���A�ͻ������������µİ����������뱣֤��������ԭ����11Сʱ��ȫ��������ϣ���A�ͻ��������ٹ�������Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2����A=��D��˵����F���C��ȵ����ɣ�
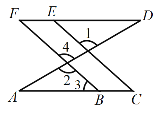
�⣺�ߡ�1=��2( ��֪ )����2=��4 ( )��
���1=��4( �������� )��
��FB��EC( )��
���3=��C( ��ֱ��ƽ�У�ͬλ����� )��
�ߡ�A=��D( )��
��ED��AC( )��
���F=��3 ( )��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У���BAC=90�����ó߹����A��һ��ֱ�ߣ�ʹ�佫��ABC�ֳ��������Ƶ������Σ�����������ȷ������ ��
A. 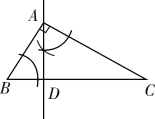 B.
B. 
C. 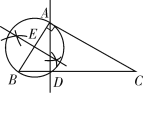 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OABC��ƽ���ı��Σ���C��x���ϣ�����������y=![]() ��x��0����ͼ����A��5��12���������BC���ڵ�D����AB=BD�����D������Ϊ_____��
��x��0����ͼ����A��5��12���������BC���ڵ�D����AB=BD�����D������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����EAF=15�㣬AB=BC=CD=DE=EF�����DEF���ڣ� ��

A.60��B.75��C.70��D.90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+c��ͼ����A����4��3����B����2��6������A���������߶Գ���ĶԳƵ�Ϊ��C����P�������߶Գ����Ҳ�ͼ���ϵ�һ�㣬��G��0����1����
��1�������C���꼰�����ߵĽ���ʽ��
��2������A��C��P��GΪ������ı����������30ʱ�����P�����ꣻ
��3����QΪ�߶�AC��һ���㣬����Qƽ����y���ֱ�������Gƽ����x���ֱ�߽��ڵ�M������QGM��QG���۵õ���QGN������N����������ʱ����Q������꣮

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com