Question

19．已知抛物线y=ax²+bx+c经过原点O及点A（-4，0）和点B（-6，3）．
（1）求抛物线的解析式以及顶点坐标；
（2）如图1，将直线y=2x沿y轴向下平移后与（1）中所求抛物线只有一个交点C，平移后的直线与y轴交于点D，求直线CD的解析式；
（3）如图2，将（1）中所求抛物线向上平移4个单位得到新抛物线，请直接写出新抛物线上到直线CD距离最短的点的坐标及该最短距离．

Answer 1

分析 （1）根据待定系数法，可得函数解析式；
（2）根据平移规律，可得直线CD的解析式，根据相切，可得关于m的方程，根据解方程，可得m；
（3）根据平移规律，可得新抛物线，根据直线与抛物线相切，可得直线MN的解析式，根据解方程组，可得G点坐标，根据垂线的关系，可得直线GH的解析式，根据解方程组，可得H点坐标，根据勾股定理，可得答案．

解答 解：（1）∵抛物线经过（0，0），（-4，0），（-6，3）三点，
∴$\left\{\begin{array}{l}c=0\\ 16a-4b=0\\ 36a-6b=3.\end{array}\right.$，
解得 $\left\{\begin{array}{l}a=\frac{1}{4}\\ b=1\\ c=0\end{array}\right.$，
∴抛物线的解析式为$y=\frac{1}{4}{x^2}+x$．
∵$y=\frac{1}{4}{x^2}+x=\frac{1}{4}（{{x^2}+4x+4-4}）=\frac{1}{4}{（{x+2}）^2}-1$，
∴抛物线的顶点坐标为（-2，-1）；
（2）设直线CD的解析式为y=2x+m，
根据题意，得$\frac{1}{4}{x^2}+x=2x+m$，
化简整理，得x²-4x-4m=0，
由△=16+16m=0，解得m=-1，
∴直线CD的解析式为y=2x-1；
（3）
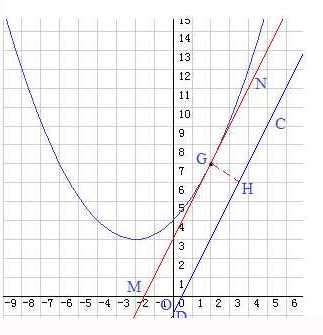
平移后的解析式为y=$\frac{1}{4}$x²+x+4  ①，
作直线MN∥CD且与平移后的抛物线切于G点，作GH⊥CD于H，
设直线MN的解析式为y=2x+n  ②，
联立①②整理，得x²-4x+16-4n=0，
∵直线MN与抛物线相切，
∴△=16-4（16-4n）=0
解得n=3
直线MN的解析式为y=2x+3  ③，
联立①③，解得x=2，y=7，
∴G（2，7），
直线GH⊥MN，
设直线GH的解析式为y=-$\frac{1}{2}$x+b′④，
将G点坐标④，得
-1+b′=7，
解得b′=8，
GH的解析式为y=-$\frac{1}{2}$x+8  ⑤，
联立GH与CD，得$\left\{\begin{array}{l}{y=2x+1}\\{y=-\frac{1}{2}x+8}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=\frac{18}{5}}\\{y=\frac{31}{5}}\end{array}\right.$，
H（$\frac{18}{5}$，$\frac{31}{5}$），
∴GH=$\sqrt{（2-\frac{18}{5}）^{2}+（7-\frac{31}{5}）^{2}}$=$\frac{4\sqrt{5}}{5}$
新抛物线上到直线CD距离最短的点的坐标（2，7），该最短距离$\frac{4\sqrt{5}}{5}$．

点评 本题考查了二次函数图象与几何变换，利用函数图象的平移规律：上移加；又利用了待定系数法求函数解析式；还利用了解方程组得出交点是解题关键．