
【题目】在△ABF中,C为AF上一点且AB=AC.
(1)尺规作图:作出以AB为直径的⊙O,⊙O分别交AC、BC于点D、E,在图上标出D、E,在图上标出D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线BF是⊙O的切线;
(3)在(2)中,若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
【答案】(1)作图见解析;(2)证明见解析;(3)BC=2![]() ,BF=
,BF=![]() .
.
【解析】试题分析:(1)作AB的垂直平分线交AB于O,以O为圆心,OA为半径作圆,⊙O即为所求;
(2)根据圆周角定理得到∠AEB=90°,根据等腰三角形的性质得到∠1=![]() ∠CAB,等量代换得到∠1=∠CBF,求出∠CBF+∠2=90°,然后,根据切线的判定即可得到结论;
∠CAB,等量代换得到∠1=∠CBF,求出∠CBF+∠2=90°,然后,根据切线的判定即可得到结论;
(3)根据已知条件得到sin∠1=![]() ,求出BE=ABsin∠1=
,求出BE=ABsin∠1=![]() ,根据勾股定理得到BC=2BE=2
,根据勾股定理得到BC=2BE=2![]() ,由勾股定理得AE=
,由勾股定理得AE=![]() =2
=2![]() ,于是得到sin∠2=
,于是得到sin∠2=![]() ,cos∠2=
,cos∠2=![]() ,根据三角函数的定义得到AG=3,根据相似三角形的性质即可得到结论.
,根据三角函数的定义得到AG=3,根据相似三角形的性质即可得到结论.
试题解析:(1)如图1,所示⊙O为所求作的圆;
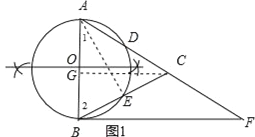
(2)连结AE,
∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°,
∵AB=AC,∴∠1=![]() ∠CAB,
∠CAB,
∵∠BAF=2∠CBF,∴∠CBF=![]() CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,
CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,
∵即∠ABF=90°,∵AB是⊙O的直径,
∴直线BF是⊙O的切线;
(3)过点C作CG⊥AB于点G,
∵sin∠CBF=![]() ,∠1=∠CBF,∴sin∠1=
,∠1=∠CBF,∴sin∠1=![]() ,
,
∵∠AEB=90°,AB=5,∴BE=ABsin∠1=![]() ,
,
∵AB=AC,∠AEB=90°,∴BC=2BE=2![]() ,
,
在Rt△ABE中,由勾股定理得AE=![]() =2
=2![]() ,∴sin∠2=
,∴sin∠2=![]() ,cos∠2=
,cos∠2=![]() ,
,
在Rt△CBG中,GC=BC sin∠2=2![]() ×
×![]() =4,GB=BCcos∠2=2,∴AG=3,
=4,GB=BCcos∠2=2,∴AG=3,
∵GC∥BF,∴△AGC∽△ABF,∴![]() ,∴BF=
,∴BF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】市政府建设一项水利工程,某运输公司承担运送总量为106m3的土石方任务,该公司有甲、乙两种型号的卡车共100辆,甲型车平均每天可以运送土石方80m3,乙型车平均每天可以运送土石方120m3,计划100天完成运输任务.
(1)该公司甲、乙两种型号的卡车各有多少台?
(2)如果该公司用原有的100辆卡车工作了40天后,由于工程进度的需要,剩下的所有运输任务必须在50天内完成,在甲型卡车数量不变情况下,公司至少应增加多少辆乙型卡车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店将某种服装按成本价提高40%后标价,又以8折优惠卖出,结果每件作服装仍可获利15元,则这种服装每件的成本是( )
A.120元
B.125元
C.135元
D.140元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10﹣14吨/月范围,并将调查结果制成了如图所示的条形统计图.

(1)请将条形统计图补充完整;
(2)这50户家庭月用水量的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
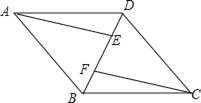
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,多宝鱼价格z(单位:元/件)与上市时间x(单位:天)的函数关系如图2所示.
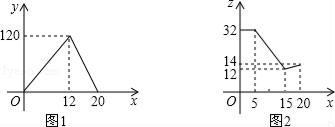
(1)观察图象,直接写出日销售量的最大值;
(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上写了一个等式:(a+3)x=4(a+3).王聪说x=4,刘敏说不一定,当x≠4时,这个等式也可能成立.你同意谁的观点?请用等式的基本性质说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对一批某品牌衬衣的质量抽检结果如下表.

(1)从这批衬衣众人抽1件是次品的概率约为多少?
(2)如果销售这批衬衣600件,那么至少要再准备多少件正品衬衣供买到次品的顾客更换?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算6+(-3.5)+(+2.5)时,较好的方法是( )
A. 按顺序进行计算B. 同号的数先相加
C. 后面的两个数先相加D. 以上的方法都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com