
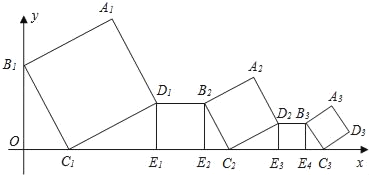
【题目】在平面直角坐标系中,正方形A1B1C1D1,D1E1E2B2,A2D2C2D2,D2E3E4B3,A3B3C3D3,…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…,在x轴上已知正方形A1,B1,C1,D1,的边长为1,∠OB1C1=30°,B1C1∥B2C2∥B3C3,…,则正方形AnBnnDn的边长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】已知函数![]() (a是常数,a≠0),下列结论正确的是( )
(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
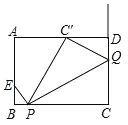
【题目】 如图,在矩形ABCD中,AB=3,BC=4,点E是边AB上一点,且AE=2EB,点P是边BC上一动点,连接EP,过点P作PQ⊥PE交射线CD于点Q.若点C关于直线PQ的对称点恰好落在边AD上,则BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
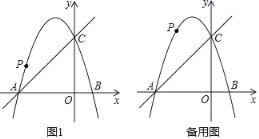
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,A点的坐标为(﹣3,0),B点在原点的左侧,与y轴交于点C(0,3),点P是直线BC上方的抛物线上一动点
(1)求这个二次函数的表达式;
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C(如图1所示),那么是否存在点P,使四边形POP′C为菱形?若存在,请此时点P的坐标:若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABCP的面积最大,并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在﹣9,﹣6,﹣3,﹣1,2,3,6,8,11这九个数中,任取一个作为a值,能够使关于x的一元二次方程x2+ax+9=0有两个不相等的实数根的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
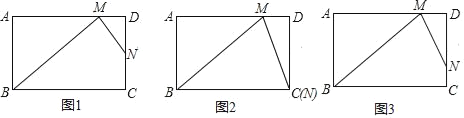
【题目】已知矩形ABCD,作∠ABC的平分线交AD边于点M,作∠BMD的平分线交CD边于点N.
(1)若N为CD的中点,如图1,求证:BM=AD+DM;
(2)若N与C点重合,如图2,求tan∠MCD的值;
(3)若![]() ,AB=6,如图3,求BC的长.
,AB=6,如图3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
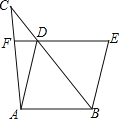
【题目】如图,在△ABC中,点D在BC边上,BC=3CD,分别过点B,D作AD,AB的平行线,并交于点E,且ED交AC于点F,AD=3DF.
(1)求证:△CFD∽△CAB;
(2)求证:四边形ABED为菱形;
(3)若DF=![]() ,BC=9,求四边形ABED的面积.
,BC=9,求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
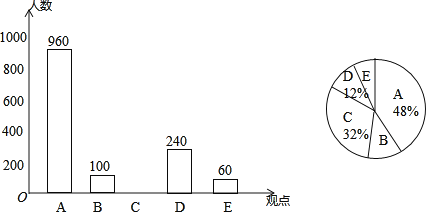
【题目】某公益机构为了解市民使用“手机阅读”的情况,对部分市民进行了随机问卷调查(问卷调查表如左图所示),并将调查结果绘制成两副统计图(均不完整)
您如何看待手机阅读问卷调查表 您好!请在表格中选择一项您最认同的观点,在其后面空格内打“√”,非常感谢您的配合. | ||
选项 | 观点 | 您的选择 |
A | 更新及时 | □ |
B | 阅读成本低 | □ |
C | 不利于人际交往 | □ |
D | 内容丰富 | □ |
E | 其他 | □ |
(1)本次接受调查的总人数是______人.
(2)请将条形统计图补充完整.
(3)在扇形统计图中,表示观点B的扇形的圆心角度数为______度.
(4)根据上述调查结果,请估计在2万名市民中,认为手机阅读“内容丰富“的大约有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com