
【题目】如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
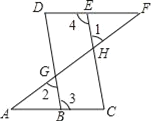
解:∵∠1=∠2(已知)
∠2=∠DGF
∴∠1=∠DGF(____________)
∴BD∥CE
∴∠3+∠C=180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( ).
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】我们约定:体重在选定标准的![]() %(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
%(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
体重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根据以上表格信息解决如下问题:
(1)将这组数据的三个统计量:平均数、中位数和众数填入下表:
平均数 | 中位数 | 众数 |
(2)请你选择其中一个统计量作为选定标准,说明选择的理由.并按此选定标准找出这10名男生中具有“一般体重”的男生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD的各顶点坐标分别为A(1,0),B(2,0),C(2,2),D(0,1),四边形BFGH的各顶点坐标分别为F(4,0),G(4,4),H(0,2),则下列说法正确的是( )

A. 四边形ABCD与四边形BFGH相似但不位似
B. 四边形ABCD与四边形BFGH位似但不相似
C. 四边形ABCD与四边形BFGH位似,且相似比为1∶![]()
D. 四边形ABCD与四边形BFGH位似,且相似比为1∶2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
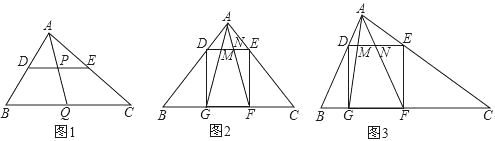
【题目】(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证: ![]() ;
;
(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DM·EN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测倾器测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.则河的宽度为________米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
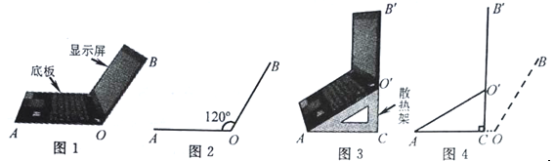
【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.
(1)求∠CAO'的度数.
(2)显示屏的顶部B'比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )

A.9 B.10 C.3![]() D.2
D.2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com