
【题目】如图,在平面直角坐标系中,点A在函数y=﹣ ![]() (x<0)的图象上,点B在函数y=
(x<0)的图象上,点B在函数y= ![]() (x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 .
(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 . 
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】某公司市场营销部的营销员的个人月收入y(元)与该营销员每月的销售量x(万件)成一次函数关系,其图象如图11所示.根据图象提供的信息,解答下列问题:
(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式;
(2)已知该公司营销员李平5月份的销售量为1.2万件,求李平5月份的收入.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的面积和对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)
【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.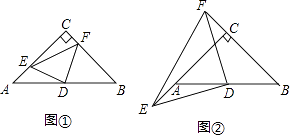
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
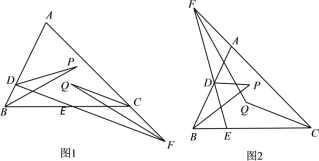
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是()

A. 10 B. ![]() C. 20 D.
C. 20 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com