
如图,直线y1=2x-3与双曲线 在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
(1)求A,B两点的坐标及k的值;
(2)请直接写出当y2>y1>0时x的取值范围.

科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:填空题
如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,PQ=3,EP=1,则DA的长是________.

查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:单选题
将0.00000305用科学记数法表示为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
如图,一圆柱高8 cm,底面半径为 cm,一只蚂蚁从点
cm,一只蚂蚁从点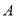 爬到点
爬到点 处吃食,要爬行的最短路程是( )cm.
处吃食,要爬行的最短路程是( )cm.

A. 6 B. 8 C. 10 D. 12
C 【解析】【解析】 底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为: ×2π×=6(cm),展开后的图形中,有BC=8cm,AC=6cm,根据勾股定理得:AB==10(cm).故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A. 25 B. 14 C. 7 D. 7或25
D 【解析】试题分析:根据直角三角形的性质可得:第三边的平方=-=7或+=25.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,BC= ,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).
,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).

查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系中,△ABC顶点A的坐标为(2,3).若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为 ,则点A′的坐标为( )
,则点A′的坐标为( )
A. (3,  ) B. (3,
) B. (3, 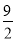 )或(-3,
)或(-3,  )
)
C. ( ,-2) D. (
,-2) D. ( ,2)或(
,2)或(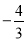 ,-2)
,-2)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学上册:第5章 一元一次方程 单元测试卷 题型:填空题
一个两位数,个位数字是十位数字的4倍,如果把个位数字与十位数字对调,那么得到的新数比原数大54,则原数为________.
28 【解析】【解析】 设原数十位数字为x,则个位数字为4x,根据题意可得: 40x+x﹣(10x+4x)=54,解得:x=2,故4x=8. 故原数为28.故答案为:28.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:解答题
某百货商店服装柜在销售中发现:某品牌童装每天可售出20件,每件盈利40元,经市场调查发现,在进货价不变的情况下,若每件童装每降价1元,日销售量将增加2件.
(1)当每件童装降价多少元时,一天的盈利最多?
(2)若商场要求一天的盈利为1200元,同时又使顾客得到实惠,每件童装降价多少元?
(1)最大值为1250元;(2)每件童装降价20元. 【解析】试题分析:(1)设每件童装降价x元,则每天盈利为S,根据盈利=(每件盈利)×(销售件数)即可解题; (2)当S=1200时,即可求得x的值,即可解题. 试题解析:(1)设每件童装降价x元,则每天盈利为S, 则S=(40﹣x)(2x+20)=﹣2x2+60x+800, 当x==15时,S有最大值为1250元;...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com