练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．使$\sqrt{-\frac{2}{x-4}}$有意义的x的取值范围是x＜4．

    分析 根据二次根式中的被开方数必须是非负数列出不等式，解不等式即可．

    解答 解：由题意得，-$\frac{2}{x-4}≥0$，
    则x-4＜0，
    解得，x＜4，
    故答案为：x＜4．

    点评 本题考查的是二次根式有意义的条件，掌握二次根式中的被开方数必须是非负数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

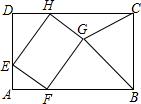    9．如图，矩形ABCD中，AD=6，CD=6+$2\sqrt{2}$，E为AD上一点，且AE=2，点F，H分别在边AB，CD上，四边形EFGH为矩形，点G在矩形ABCD的内部，则当△BGC为直角三角形时，AF的值是2或4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．若?ABCD的三条边分别为8cm，（x-2）cm，（x+3）cm，则该?ABCD的周长是22或42cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

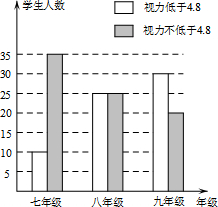    7．在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图．请根据图中信息解决下列问题：
    （1）本次抽查活动中共抽查了145名学生；
    （2）已知该校七年级、八年级、九年级学生数分别为360人、400人、540人．
    ①估算：该校九年级视力不低于4.8的学生约有216名；
    ②为了估算出该校视力低于4.8的学生数，小明是这样计算的：
    步骤一：计算样本中视力低于4.8的学生比例：
    $\frac{10+25+30}{（10+35）+（25+25）+（30+20）}$×100%≈44.83%．
    步骤二：用样本估计总体，从而求得全校视力低于4.8的学生数：
    （360+400+540）×44.83%≈583（名）．
    请你判断小明的估算方法是否正确？如果正确，请你计算出扇形统计图中“视力低于4.8”的圆心角的度数；如果不正确，请你帮忙估算出该校视力低于4.8的学生数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．在一个不透明布袋里面装有11个球，其中有4个红球，7个白球，每个球除颜色外其他完全相同，从中任意摸出一个球，是白球的概率是$\frac{7}{11}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某数学老师为了了解学生在数学学习中常见错误的纠正情况，收集整理了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对他所教的初三（1）班（2）班进行了检测．如图表示从两班各随机抽取的10名学生的得分情况：
    （1）利用图中提供的信息，补全下表：
    班级平均数（分）中位数（分）众数（分）
    （1）班24 2424 
    （2）班   2424    21
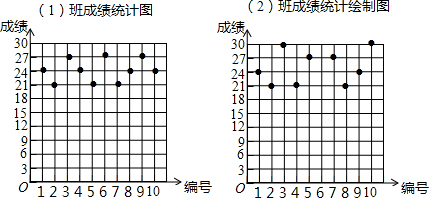
    （2）若把24分以上（含24分）记为”优秀”，两班各50名学生，请估计两班各有多少名学生成绩优秀；
    （3）观察图中数据分布情况，请通过计算说明哪个班的学生纠错的得分情况更稳定．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在一个不透明的袋子中装有三张分别标有1、2、3数字的卡片（卡片除数字外完全相同）．
    （1）从袋中任意抽取一张卡片，则抽出的是偶数的概率为$\frac{1}{3}$；
    （2）从袋中任意抽取二张卡片，求被抽取的两张卡片构成两位数是奇数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

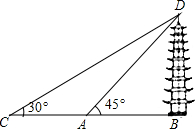    8．五一节，某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观，并测量其高度．如图，塔身BD与地面垂直，他们先在A处测得塔顶端点D的仰角为45°，再沿着BA的方向后退16cm至C处，测得塔顶端点D的仰角为30°，求“海春轩塔”BD的高度．（$\sqrt{3}$≈1.73，结果保留一位小数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，在菱形ABCD中，∠BCD=108°，CD的垂直平分线交对角线AC于点F，E为垂足，连结BF，则∠ABF等于18°．

    查看答案和解析>>

    同步练习册答案