
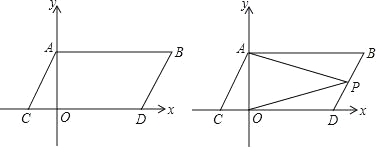
【题目】如图,在平面直角坐标系中,A、B坐标分别为A(O,a)、B(b,a),且a、b满足:![]() ,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.
,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.
(1)求点C、D的坐标;
(2)在y轴上是否存在点M,连接MC、MD,使三角形MCD的面积为30?若存在这样的点,求出点M的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA、PO,当点P在BD上移动时(不与B、D重合),![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
【答案】(1)点C(﹣1,0),D(4,0);(2)存在,点M(0,12)或(0,﹣12);(3)![]() 不变,理由见解析.
不变,理由见解析.
【解析】
(1)由偶次方及算术平方根的非负性可求出a、b的值,进而即可得出点A、B的坐标,再根据平移的性质可得出点C、D的坐标;
(2)设存在点M(0,y),根据三角形的面积结合S△MCD=30,即可得出关于y的含绝对值符号的一元一次方程,解之即可得出结论;
(3)过P点作PE∥AB交OC与E点,根据平行线的性质得∠BAP+∠DOP=∠APE+∠OPE=∠APO,故比值为1.
(1)∵![]() ,
,
∴a=3,b=5,
∴点A(0,3),B(5,3).
将点A,B分别向下平移3个单位,再向左平移1个单位,得到点C、D,
∴点C(﹣1,0),D(4,0).
(2)设存在点M(0,y),
根据题意得:S△MCD=![]() ×5|y|=30,
×5|y|=30,
∴解得:y=±12,
∴存在点M(0,12)或(0,﹣12).
(3)当点P在BD上移动时,![]() =1不变,理由如下:
=1不变,理由如下:
过点P作PE∥AB交OA于E,
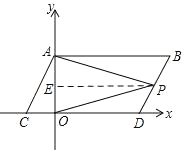
∵CD由AB平移得到,则CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
∴![]() =1.
=1.


科目:初中数学 来源: 题型:
【题目】一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
![]()
(1)求高铁列车的速度和AB两站之间的距离.(2)如果高铁列车从A站出发,开出多久可以到达C站?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,3),B(b,1)都在双曲线y= ![]() 上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一可以自由转动的转盘,AB为转盘直径,如图所示,并规定:顾客消费100元(含100元)以上,就能获得一次转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,顾客就可以获得相应的优惠.
(1)某顾客正好消费99元,是否可以获得相应的优惠.
(2)某顾客正好消费120元,他转一次转盘获得三种打折优惠的概率分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
科目:初中数学 来源: 题型:
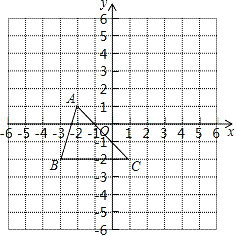
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=﹣x+1(0≤x≤10)与反比例函数y= ![]() (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A.﹣ ![]() ≤x≤1
≤x≤1
B.﹣ ![]() ≤x≤
≤x≤ ![]()
C.﹣ ![]() ≤x≤
≤x≤ ![]()
D.1≤x≤ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com