
【题目】下列条件中,不能判定一个四边形是平行四边形的是( )
A. 两组对边分别平行B. 一组对边平行且相等C. 两组对角分别相等 D. 一组对边相等且一组对角相等
【答案】D
【解析】
根据平行四边形的判定方法逐一进行判断即可.
A. 两组对边分别平行的四边形是平行四边形,故A选项正确,不符合题意;
B. 一组对边平行且相等的四边形是平行四边形,故B选项正确,不符合题意;
C. 两组对角分别相等的四边形是平行四边形,故C选项正确,不符合题意;
D. 一组对边相等且一组对角相等的四边形不一定是平行四边形,
如图,四边形ABCD为平行四边形,连接AC,作AE垂直BC于E,
在EB上截取EC'=EC,连接AC',则△AEC'≌△AEC,AC'=AC,
把△ACD绕点A顺时针旋转∠CAC'的度数,则AC与AC'重合,
显然四边形ABC'D'满足:AB=CD=C'D',∠B=∠D=∠D',而四边形ABC'D'并不是平行四边形,故D选项错误,符合题意,

故选D.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉。例如:|6+7|= 6+7 ;|6—7|=7- 6;|7-6|=7- 6 ;|―6―7|=6+7;根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=______;
(2)|![]() |=_______;
|=_______;
(3)|![]() |=________;
|=________;
(4)用合理的方法计算:|![]() |+|
|+|![]() |-|
|-|![]() |.
|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=![]() (k≠0)的图象过点C,则该反比例函数的表达式为_______.
(k≠0)的图象过点C,则该反比例函数的表达式为_______.
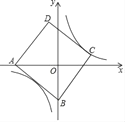
【答案】![]()
【解析】解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,∴∠ABO+∠CBE=90°,∵∠OAB+∠ABO=90°,∴∠OAB=∠CBE,∵点A的坐标为(﹣4,0),∴OA=4,∵AB=5,∴OB=![]() =3,在△ABO和△BCE中,∵∠OAB=∠CBE,∠AOB=∠BEC,AB=BC,∴△ABO≌△BCE(AAS),∴OA=BE=4,CE=OB=3,∴OE=BE﹣OB=4﹣3=1,∴点C的坐标为(3,1),∵反比例函数
=3,在△ABO和△BCE中,∵∠OAB=∠CBE,∠AOB=∠BEC,AB=BC,∴△ABO≌△BCE(AAS),∴OA=BE=4,CE=OB=3,∴OE=BE﹣OB=4﹣3=1,∴点C的坐标为(3,1),∵反比例函数![]() (k≠0)的图象过点C,∴k=xy=3×1=3,∴反比例函数的表达式为
(k≠0)的图象过点C,∴k=xy=3×1=3,∴反比例函数的表达式为![]() .故答案为:
.故答案为: ![]() .
.

点睛:本题考查的是反比例函数图象上点的坐标特点,涉及到正方形的性质,全等三角形的判定与性质,反比例函数图象上的点的坐标特征,作辅助线构造出全等三角形并求出点D的坐标是解题的关键.
【题型】填空题
【结束】
17
【题目】关于x的分式方程![]() =1的解是正数,则m的取值范围是_____.
=1的解是正数,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
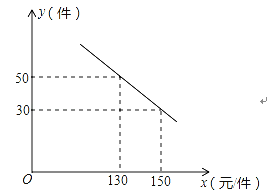
【题目】电商时代使得网购更加便捷和普及.小张响应国家号召,自主创业,开了家淘宝店.他购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.
(1)求y与x之间的函数关系式;
(2)若某天小张销售该产品获得的利润为1200元,求销售单价x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5![]() ﹣(﹣2
﹣(﹣2![]() )+(﹣3
)+(﹣3![]() )﹣(+4
)﹣(+4![]() )
)
(2)(﹣![]() ﹣
﹣![]() +
+![]() )×(﹣24)
)×(﹣24)
(3)(﹣3)÷![]() ×
×![]() ×(﹣15)
×(﹣15)
(4)﹣14+|(﹣2)3﹣10|﹣(﹣3)÷(﹣1)2017.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
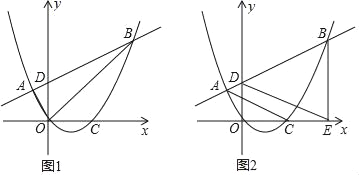
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
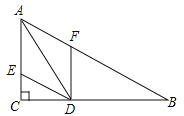
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
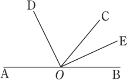
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC的平分线,
所以∠COE=![]() .
.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知
∠BOE=∠COE= ﹣∠COD= °.
所以∠AOE= ﹣∠BOE= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com