
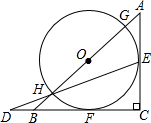
 如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D.
如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D.分析 (1)连接OE、OF,由切线的性质结合结合直角三角形可得到正方形OECF,由等腰直角三角形△ABC证得△AEO是等腰直角三角形,即问题可得;
(2)再由切割线定理可得BF2=BH•BG,利用方程即可求出BH,然后又因OE∥DB,OE=OH,利用相似三角形的性质即可求出BH=BD,最终由CD=BC+BD,即可求出答案.
解答 解:(1)如图,连接OE、OF,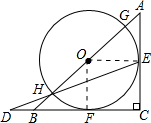
∵由切线的性质可得OE=OF=⊙O的半径,∠OEC=∠OFC=∠C=90°,
∴四边形OECF是正方形,
∴CE=OF,
∵∠ACB=90°,AC=BC,
∴∠A=45°,
∵∠AEO=90°,
∴∠AOE=45°,
∴AE=OE,
∴AE=CE;
(2)设⊙O的半径为r,则OE=r,OB=$\sqrt{2}$r,BG=($\sqrt{2}$+1)r,BF=OF=r,BC=2r,
由切割线定理可得BF2=BH•BG,
∴r2=BH($\sqrt{2}$+1)r,
∴BH=($\sqrt{2}$-1)r,(负值舍去)
∵OE∥DB,OE=OH,
∴△OEH∽△BDH,
∴$\frac{OE}{OH}$=$\frac{BD}{BH}$=1,
∴BH=BD,CD=BC+BD=2r+($\sqrt{2}$-1)r=($\sqrt{2}$+1)r,
∴tan∠DEC=$\sqrt{2}$+1.
点评 本题考查了正方形的判定和性质、勾股定理、等腰直角三角形的性质、平行线分线段成比例定理的推论、相似三角形的判定和性质、切线的性质.解题的关键是构造正方形CEOF.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
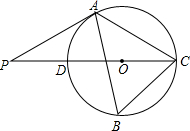 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
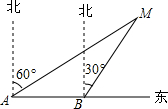 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )| A. | 10分钟 | B. | 15分钟 | C. | 20分钟 | D. | 25分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
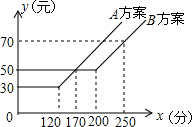 如图是某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的共有( )
如图是某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
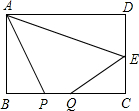 如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点,
如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com