
����Ŀ��Ϊ��Ӧ������֯����ġ���̼����ĺ��٣��������������������������г��ϰ࣮��һ�죬���������г��Ӽ��ﵽ�����ϰ࣬;�������г��������ϣ���������һ��ʱ�䣬���ú�������У�ֱ�����﹤���������������г�������������ʻ����������ҵľ���![]() ���ף������ʱ��
���ף������ʱ��![]() �����ӣ��Ĺ�ϵ��ʾ����ͼ��
�����ӣ��Ĺ�ϵ��ʾ����ͼ��
��1�������Ӽҳ��������ֹ���ʱ���ٶ�Ϊ �ף����ӣ�
��2����������ʱ ���ӣ�
��3�����߶�BC����Ӧ�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������������ڽǶ����ı�Ϊ2�U7�U4����ô����������ǣ��� ��
A.ֱ��������
B.���������
C.�۽�������
D.�ȱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
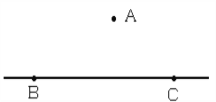
����Ŀ����ͼ�����ٹ�·BC����·��Ϊֱ�ߣ����������Ϊ120![]() ���ڸù�·���Ϸ������20
���ڸù�·���Ϸ������20![]() �ĵ�A��������һ�������ǣ���֪�ڵ�A��õ�B�ĸ���Ϊ45�㣬��C�ĸ���Ϊ30�㣬�����Ǽ�һ�������ӵ�B������ʻ����C���õ�ʱ����1.5
�ĵ�A��������һ�������ǣ���֪�ڵ�A��õ�B�ĸ���Ϊ45�㣬��C�ĸ���Ϊ30�㣬�����Ǽ�һ�������ӵ�B������ʻ����C���õ�ʱ����1.5![]() ����ͨ�����㣬�о����������������·���Ƿ��٣����ο����ݣ�
����ͨ�����㣬�о����������������·���Ƿ��٣����ο����ݣ� ![]() ��1.7��
��1.7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD�У�AB��DC����D=90o��AC��BC��AB=10![]() ,BC=6
,BC=6![]() ��F����2
��F����2![]() ��
��![]() ���ٶ����߶�AB����A��B�����˶���E��ͬʱ��1
���ٶ����߶�AB����A��B�����˶���E��ͬʱ��1![]() ��
��![]() ���ٶ����߶�BC����B��C�����˶������˶�ʱ��Ϊ
���ٶ����߶�BC����B��C�����˶������˶�ʱ��Ϊ![]() ��(0��
��(0��![]() ��5)��
��5)��
��1����֤����ACD�ס�BAC�� ��2����DC�ij���
��3�����ı���AFEC�����Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() ����Сֵ��
����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�����Σ���C������Ϊ��4��0������AOC=60������ֱ��x���ֱ��l��y���������x����������ÿ��1����λ���ȵ��ٶ�����ƽ�ƣ���ֱ��l������OABC�����߷ֱ��ڵ�M��N����M�ڵ�N���Ϸ���������OMN�����ΪS��ֱ��l���˶�ʱ��Ϊt �루0��t��4�������ܴ��·�ӳS��t�ĺ�����ϵ��ͼ���ǣ� ��
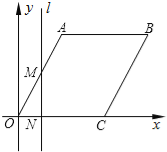
A.  B.
B. 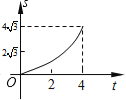
C.  D.
D. 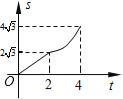
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0��������A����3��0����B��1��0����C����2��1������y���ڵ�M��
��a��0��������A����3��0����B��1��0����C����2��1������y���ڵ�M��
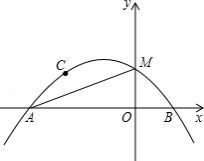
��1���������ߵı���ʽ��
��2��DΪ�������ڵڶ��������ϵ�һ�㣬��DE��ֱx���ڵ�E�����߶�AM�ڵ�F�����߶�DF���ȵ����ֵ�������ʱ��D�����ꣻ
��3�����������Ƿ����һ��P����PN��ֱx���ڵ�N��ʹ���Ե�P��A��NΪ���������������MAO���ƣ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С����������һ���йؽ�ƽ���ߵ����⣺��ͼ1���ڡ�ABC�У���A=2��B��CDƽ�֡�ACB��AD=2.2��AC=3.6
��BC�ij���
С��˼������ΪCDƽ�֡�ACB�����Կ���BC����ȡ��E��ʹEC=AC������DE�����������õ���DEC�ա�DAC������������ʹ����õ��������ͼ2����
��ش�
��1����BDE��
��2��BC�ij�Ϊ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com