
【题目】如图,在菱形ABCD中,点M、N在直线BD上,点M在N点左侧,AM∥CN.
(1)如图1,求证:BM=DN;
(2)如图2,当∠ABC=90°,点M,N在线段BD上时,求证:BM+BN= ![]() AB;
AB;
(3)如图3,当∠ABC=60°,点M在线段DB的延长线上时,直接写出BM,BN,AB三者的数量关系.
【答案】
(1)
解:∵四边形ABCD为菱形,
∴AB=CD,AB∥CD.
∴∠ABM=∠CDN.
∵AM∥CN,
∴∠AMN=∠MNC.
∴∠AMB=∠CND.
在△AMB和△CND中, 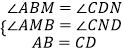
∴△AMB≌△CND.
∴MB=DN
(2)
解:由(1)得BM=DN.
∴BN+BM=DB.
当∠ABC=90°时,由勾股定理得;BD= ![]() =
= ![]() =
= ![]() AB.
AB.
∴MB+BN= ![]() AB
AB
(3)
解:NB﹣BM= ![]() AB.
AB.
如图1所示:过点A作AE⊥MN,垂足为E.
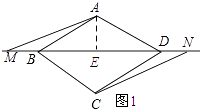
由(1)得BM=DN.
又∵BD=BN﹣DN,
∴BD=BN﹣BM.
当∠ABC=60°时,∠ABE=30°,
又∵∠AEB=90°,
∴AE= ![]() AB.
AB.
∴在Rt△ABE中,BE= ![]() =
= ![]() =
= ![]() AB.
AB.
∵AB=AD,AE⊥BD,
∴BE=ED.
∴BD= ![]() AB.
AB.
∴BN﹣BM= ![]() AB.
AB.
由勾股定理得;BD= ![]() =
= ![]() =
= ![]() AB.
AB.
∴MB+BN= ![]() AB
AB
【解析】(1)由菱形的性质可知AB=CD,AB∥CD,然后由平行线的性质和补角的性质∠ABM=∠CDN,∠AMB=∠CND,接下来依据AAS证明△AMB≌△CND,由全等三角形的性质可得到MB=DN;(2)由(1)得BM=DN,故此可得到BN+BM=DB,当∠ABC=90°时,在Rt△ABD中,由勾股定理可求得BD与AB的关系,从而得到BM+BN= ![]() AB;(3)过点A作AE⊥MN,垂足为E.由BM=DN可证明BD=BN﹣BM,当∠ABC=60°时,∠ABE=30°在Rt△ABE中,依据勾股定理可求得BE与AB的关系,然后再依据等腰三角形三线合一的性质可得到AB与BD的关系,于是得到BM,BN,AB三者的数量关系.
AB;(3)过点A作AE⊥MN,垂足为E.由BM=DN可证明BD=BN﹣BM,当∠ABC=60°时,∠ABE=30°在Rt△ABE中,依据勾股定理可求得BE与AB的关系,然后再依据等腰三角形三线合一的性质可得到AB与BD的关系,于是得到BM,BN,AB三者的数量关系.
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2016年里约奥运会后,同学们参与体育锻炼的热情高涨,为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下频数分布表和扇形统计图。根据上述信息解答下列问题:
(1)m=____,n=____;
(2)在扇形统计图中,D组所占圆心角的度数是____;
(3)全校共有3000名学生,该校平均每周体育锻炼时间不少于6小时的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F. 
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点E,F分别在射线AB,射线BC上,AE=BF,DE与AF交于点O.
(1)如图1,当点E,F分别在线段AB,BC上时,则线段DE与AF的数量关系是 ,位置关系是 .
(2)如图2,当点E在线段AB延长线上时,将线段AE沿AF进行平移至FG,连接DG.
①依题意将图2补全;
②小亮通过观察、实验提出猜想:在点E运动的过程中,始终有![]() .
.
小亮把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:连接EG,要证明![]() ,只需证四边形FAEG是平行四边形及△DGE是等腰直角三角形.
,只需证四边形FAEG是平行四边形及△DGE是等腰直角三角形.
想法2:延长AD,GF交于点H,要证明![]() ,只需证△DGH是直角三角形.
,只需证△DGH是直角三角形.

图1 图2
请你参考上面的想法,帮助小亮证明![]() .(一种方法即可)
.(一种方法即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com