
分析 分两种情况解答:①AC为斜边,BC,AB为直角边;②BC为斜边,AC,AB为直角边;根据勾股定理计算即可.
解答 解:①AC为斜边,BC,AB为直角边,
由勾股定理得BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$;
②BC为斜边,AC,AB为直角边,
由勾股定理得BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5;
所以BC的长为$\sqrt{7}$或5.
故答案为:$\sqrt{7}$或5.
点评 本题考查的是勾股定理,解答此题时要注意进行分类讨论,不要漏解.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
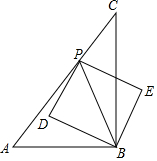 定义,若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”,如图,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA-AB以5cm/s的速度运动,当电P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
定义,若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”,如图,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA-AB以5cm/s的速度运动,当电P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 互余但不相等 | B. | 互为补角 | C. | 相等但不互余 | D. | 互余且相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
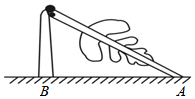 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )
如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )| A. | 10m | B. | 15m | C. | 18m | D. | 20m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
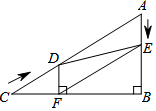 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx(a≠0)经过A(4,4)、B(2,-2)两点,与x轴交于点C.
如图,已知抛物线y=ax2+bx(a≠0)经过A(4,4)、B(2,-2)两点,与x轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com