
【题目】如图1,在菱形ABCD中,AC=2,BD=2![]() ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.

【答案】(1)2 (2)①等边三角形 ②![]()
【解析】试题分析:(1)∵四边形ABCD是菱形,
∴△AOB为直角三角形,且OA=![]() AC=1,OB=
AC=1,OB=![]() BD=
BD=![]() .
.
在Rt△AOB中,由勾股定理得:
AB=![]() =
=![]() =2.
=2.
(2)①△AEF是等边三角形.理由如下:
∵由(1)知,菱形边长为2,AC=2,
∴△ABC与△ACD均为等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,又∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF.
在△ABE与△ACF中,
∵ ,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∴△AEF是等腰三角形,
又∵∠EAF=60°,
∴△AEF是等边三角形.
②BC=2,E为四等分点,且BE>CE,
∴CE=![]() ,BE=
,BE=![]() .
.
由①知△ABE≌△ACF,
∴CF=BE=![]() .
.
∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°(三角形内角和定理),
∠AEG=∠FCG=60°(等边三角形内角),
∠EGA=∠CGF(对顶角)
∴∠EAC=∠GFC.
在△CAE与△CFG中,
∵![]() ,
,
∴△CAE∽△CFG(AA),
∴![]() ,即
,即![]() ,
,
解得:CG=![]() .
.


科目:初中数学 来源: 题型:
【题目】实践探究,解决问题
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD . 
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=;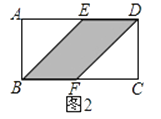
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD之间满足的关系式为;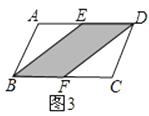
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.
解决问题: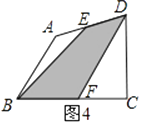
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).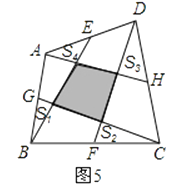
查看答案和解析>>
科目:初中数学 来源: 题型:
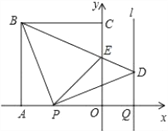
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)6.25×(﹣3.4)+6.25×4.4
(3)![]()
(4)![]()
(5)(﹣1)2015﹣(1﹣0.5)2×|2﹣22|
(6)﹣1+2﹣3+4﹣…﹣2015+2016.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com