
分析 先利用甲的方法,根据根的判别式△=4p2-4>0可得出p的取值范围,再设方程的两根为x1,x2,利用根与系数的关系找出两根之和与两根之积,利用乙的方法将不等式进行变形,代入数据即可得出p的取值范围,综合甲乙的结论即可得出结果.
解答 解:∵方程x2+2px+1=0有两个不相等的实数根,
∴△=(2p)2-4×1×1=4p2-4>0,
∴p>1或p<-1.
设方程的两根为x1,x2,由题意可得:
(x2-1)(x1-1)<0,
∵x1+x2=-2p,x1•x2=1,
∴(x2-1)(x1-1)=x1•x2-(x1+x2)+1=2+2p<0,
解得:p<-1.
∴p<-1.
点评 本题考查了根的判别式以及根与系数的关系,解题的关键是分别利用甲乙的方法找出p的取值范围.本题属于中档题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积是关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
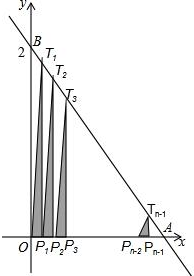 如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n段,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{2015}{4032}$.
如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n段,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{2015}{4032}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
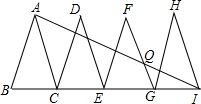 如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=$\frac{4}{3}$.
如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com