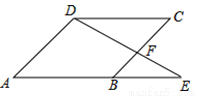
如图,E为平行四边形ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则平行四边形ABCD的面积为() A. 30 B. 27 C. 14 D. 32 A [解析]∵四边形ABCD是平行四边形. ∴AB//CD.AB=CD.AD//BC. ∴△BEF∽△CDF.△BEF∽△AED. ∴ . ∵BE:AB=2:3.AE=AB+BE. ∴BE:CD=2:3.BE: 题目和参考答案——青夏教育精英家教网—

如图,E为平行四边形ABCD的边AB延长线上的一点,且BE:AB=2：3,△BEF的面积为4,则平行四边形ABCD的面积为()

A. 30 B. 27 C. 14 D. 32

A 【解析】∵四边形ABCD是平行四边形， ∴AB//CD，AB=CD，AD//BC， ∴△BEF∽△CDF，△BEF∽△AED， ∴ ， ∵BE：AB=2：3，AE=AB+BE， ∴BE：CD=2：3，BE：AE=2：5， ∴ ， ∵S△BEF=4， ∴S△CDF=9，S△AED=25， ∴S四边形ABFD=S△AED-S△BEF=25...

练习册系列答案

天天练习王口算题卡口算速算巧算系列答案

育才课堂教学案系列答案

新课标教材同步导练绩优学案系列答案

智慧鸟单元评估卷系列答案

中考必备河南中考试题精选精析卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：湖北省襄阳市襄城区2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

下列各方程，变形正确的是（）

A. 化为

B. 化为

C. 化为

D. 化为

D 【解析】试题解析：A、-=1化为x=-3，故此选项错误； B、1-[x-（2-x）]=x化为3x=-3，故此选项错误； C、化为3x-2x+2=6，故此选项错误； D、化为2（x-3）-5（x+4）=10，此选项正确．故选D．

查看答案和解析>>

科目：初中数学 来源：2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型：解答题

（1）计算：8x4y2÷x3y×2x．（2）计算：(2x＋5)( 3x－7) ．

（1）16x2y;（2）6x2＋x－35．【解析】试题分析：（1）先计算单项式除以单项式，再计算单项式乘以单项式即可得出结果；（2）运用多项式乘以多项式的运算法则进行计算即可. 试题解析：（1） 8x4y2÷x3y×2x =8xy×2x =16x2y．（2） (2x＋5)( 3x－7) =6x2－14x＋15x－35 =6x2＋x－35． ...

查看答案和解析>>

科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型：解答题

某研究所将某种材料加热到1000℃时停止加热，并立即将材料分为A、B两组，采用不同工艺做降温对比实验，设降温开始后经过x min时，A、B两组材料的温度分别为yA℃、yB℃，yA、yB与x的函数关系式分别为yA=kx+b，yB=（x﹣60）2+m（部分图象如图所示），当x=40时，两组材料的温度相同．

（1）分别求yA、yB关于x的函数关系式；

（2）当A组材料的温度降至120℃时，B组材料的温度是多少？

（3）在0＜x＜40的什么时刻，两组材料温差最大？

【答案】（1）yA=﹣20x+1000；

（2）B组材料的温度是164℃；

（3）当x=20时，两组材料温差最大为100℃．

【解析】试题分析：（1）首先求出yB函数关系式，进而得出交点坐标，即可得出yA函数关系式；（2）首先将y=120代入求出x的值，进而代入yB求出答案；（3）得出yA-yB的函数关系式，进而求出最值即可．

试题解析：（1）由题意可得出：yB=（x﹣60）2+m经过（0，1000），

则1000=（0﹣60）2+m，

解得：m=100，

∴yB=（x﹣60）2+100，

当x=40时，yB=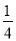×（40﹣60）2+100，

解得：yB=200，

yA=kx+b，经过（0，1000），（40，200），

则，

解得：，

∴yA=﹣20x+1000；

（2）当A组材料的温度降至120℃时，

120=﹣20x+1000，

解得：x=44，

当x=44，yB=（44﹣60）2+100=164（℃），

∴B组材料的温度是164℃；

（3）当0＜x＜40时，yA﹣yB=﹣20x+1000﹣（x﹣60）2﹣100=﹣x2+10x=﹣（x﹣20）2+100，

∴当x=20时，两组材料温差最大为100℃．

【题型】解答题
【结束】
26

正方形ABCD的边长为6cm，点E，M分别是线段BD，AD上的动点，连接AE并延长，交边BC于F，过M作MN⊥AF，垂足为H，交边AB于点N.

(1)如图①，若点M与点D重合，求证：AF＝MN；

(2)如图②，若点M从点D出发，以1cm/s的速度沿DA向点A运动，同时点E从点B出发，以cm/s的速度沿BD向点D运动，运动时间为ts.

①设BF＝ycm，求y关于t的函数表达式；

②当BN＝2AN时，连接FN，求FN的长．

见解析【解析】试题分析：（1）根据四边形的性质得到AD=AB，∠BAD=90°，由垂直的定义得到∠AHM=90°，由余角的性质得到∠BAF=∠AMH，根据全等三角形的性质即可得到结论；（2）①根据勾股定理得到BD=6，由题意得，DM=t，BE=t，求得AM=6-t，DE=6-t，根据相似三角形的判定和性质即可得到结论； ②根据已知条件得到AN=2，BN=4，根据相似三角形的性...

查看答案和解析>>

科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型：解答题

计算：3tan30°＋cos245°－2sin60°．

【解析】试题分析：本题可根据特殊的三角函数值解出tan30°、cos45°、sin60°的值，再代入原式中即可．试题解析：原式=3×+-2×， =， =.

查看答案和解析>>

科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型：单选题

如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若BO=6cm,OC=8cm 则BE+CG的长等于( )

A. 13 B. 12 C. 11 D. 10

D 【解析】根据切线长定理得：BE=BF，CF=CG，∠OBF=∠OBE，∠OCF=∠OCG； ∵AB∥CD， ∴∠ABC+∠BCD=180°， ∴∠OBF+∠OCF=90°， ∴∠BOC=90°， ∵OB=6cm，OC=8cm， ∴BC=10cm， ∴BE+CG=BC=10cm，故选D.

查看答案和解析>>

科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型：单选题

点A(-2,5)在反比例函数y= (k0)的图象上,则k的值是( )

A. B. C. -10 D. -5

C 【解析】把（-2，5）代入y=，得：，解得：k=-10，故选C.

查看答案和解析>>

科目：初中数学 来源：广东省深圳市龙岗区2017-2018学年度第一学期期末质量检测八年级数学试卷 题型：单选题

深圳空气质量优良指数排名近年来一直排在全国城市前十.下表是深圳市气象局于2016年3月22日在全市十一个监测点监测到空气质量指数（AQI）数据：

监测点	荔园	西乡	华侨城	南油	盐田	龙岗	洪湖	南澳	葵涌	梅沙	观澜
AQI	15	31	25	24	31	24	25	25	34	20	26
质量	优	优	优	优	优	优	优	优	优	优	优

上述（AQI）数据中，众数和中位数分别是（）

A. 25,25 B. 31,25 C. 25,24 D. 31,24

A 【解析】试题分析：一组数据中出现次数最多的数据叫做众数；把这组数据按照从小到大的顺序排列，第6个数是中位数．因此把这组数据按照从小到大的顺序排列15，20，24，24，25，25，25，26，31，31，34，第6个数是25，所以中位数是25；在这组数据中出现次数最多的是25，即众数是25．故选A．

查看答案和解析>>

科目：初中数学 来源：江苏省扬州市2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

如图是由一些棱长都为1cm的小正方体组合成的简单几何体．

（1）该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；

（2）如果在这个几何体上再添加一些小正方体，并保持俯视图和左视图不变，最多可以再添加　　块小正方体．

（1）作图见解析；（2）6. 【解析】试题分析：(1)、根据长对正，高平齐和宽相等的法则画出三视图；(2)、根据三视图的法则得出立体图形，从而得出答案．试题解析：【解析】（1）如图所示：；（2）保持俯视图和左视图不变，最多可以再添加6块小正方体.

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学