
”¾ĢāÄæ”æ(1)ŅŌĻĀĮŠÕż·½ŠĪĶųĀēµÄ½»µćĪŖ¶„µć£¬·Ö±š»³öĮ½øöĻąĖĘ±Č²»ĪŖ1µÄĻąĖĘČż½ĒŠĪ£¬Ź¹ĖüĆĒ£ŗ¢Ł¶¼ŹĒÖ±½ĒČż½ĒŠĪ£»¢Ś¶¼ŹĒČń½ĒČż½ĒŠĪ£»¢Ū¶¼ŹĒ¶Ū½ĒČż½ĒŠĪ£®
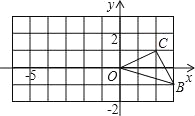
(2)ČēĶ¼£¬ŅŃÖŖOŹĒ×ų±źŌµć£¬B”¢CĮ½µćµÄ×ų±ź·Ö±šĪŖ(3£¬©1)”¢(2£¬1)£®
¢ŁŅŌ0µćĪŖĪ»ĖĘÖŠŠÄŌŚyÖįµÄ×ó²ą½«”÷OBC·Å“óµ½Į½±¶(¼“ŠĀĶ¼ÓėŌĶ¼µÄĻąĖʱČĪŖ2)£¬»³öĶ¼ŠĪ£»
¢Ś·Ö±šŠ“³öB”¢CĮ½µćµÄ¶ŌÓ¦µćB”䔢C”äµÄ×ų±ź£»
¢ŪČē¹ū”÷OBCÄŚ²æŅ»µćMµÄ×ų±źĪŖ(x£¬y)£¬Š“³öMµÄ¶ŌÓ¦µćM”äµÄ×ų±ź£®
”¾“š°ø”æ(1)¼ū½āĪö£»(2)¢Ł¼ū½āĪö£»¢ŚB”ä(©6£¬2)£¬C”ä(©4£¬©2)£»¢ŪM”ä(©2x£¬©2y)£®
”¾½āĪö”æ
£Ø1£©°“ĢāÖŠŅŖĒó»³öĶ¼ŠĪ¼“æÉ£»
£Ø2£©ÓÉĢāŅā»³öĶ¼ŠĪ£¬ÓÉÓŚŹĒ½«”÷OBC·Å“óµ½Į½±¶£¬ĖłŅŌĒ°ŗóĮ½øöČż½ĒŠĪŹĒĪ»ĖĘĶ¼ŠĪ£¬æɹżµćC£¬B·“ĻņŃÓ³¤BO£¬CO£¬Ź¹µĆOB”ä=2OB£¬OC”ä=2OC£¬¼“Ź¹µĆµ½µÄČż½ĒŠĪŹĒŌĄ“µÄ2±¶¼“æÉ£¬ŅņĪŖĘä¹ŲÓŚŌµć¶Ō³Ę£¬ĒŅB£¬CµćµÄ×ų±źŅŃÖŖ£¬½ų¶ųæÉµĆ³öĘä¶ŌÓ¦µćµÄ×ų±ź£¬ÓÉÓŚµćMŌŚČż½ĒŠĪÖŠ£¬ĖłŅŌĘä¶ŌÓ¦µćŅ²¹ŲÓŚŌµć¶Ō³Ę£¬ÓÉMµÄ×ų±ź£¬½ų¶ųæɵĆĘä¶ŌÓ¦µćµÄ×ų±ź£®
½ā£ŗ(1)
¢Ł¶¼ŹĒÖ±½ĒČż½ĒŠĪ
¢Ś¶¼ŹĒČń½ĒČż½ĒŠĪ
¢Ū¶¼ŹĒ¶Ū½ĒČż½ĒŠĪ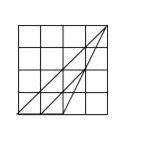 £»
£»
(2) ¢ŁČēĶ¼
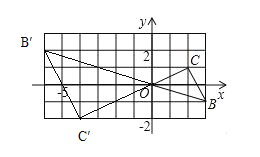
¢ŚB”äµÄ×ų±źĪŖ(©6£¬2)£¬C”äµÄ×ų±źĪŖ(©4£¬©2)£¬
¢Ū”ßMµÄ×ų±źĪŖ(x£¬y)£¬
”ąM”äµÄ×ų±źĪŖ(©2x£¬©2y)£®
¹Ź“š°øĪŖ£ŗ(1)¼ū½āĪö£»(2)¢Ł¼ū½āĪö£»¢ŚB”ä(©6£¬2)£¬C”ä(©4£¬©2)£»¢ŪM”ä(©2x£¬©2y)£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĻĀĶ¼£¬ŅŃÖŖ”ŃOµÄÖ±¾¶ĪŖAB£¬AC”ĶABÓŚµćA, BCÓė”ŃOĻą½»ÓŚµćD£¬ŌŚACÉĻČ”Ņ»µćE£¬Ź¹µĆED=EA£®ĻĀĆęĖÄøö½įĀŪ£ŗ¢ŁEDŹĒ”ŃOµÄĒŠĻߣ»¢ŚBC=2OE¢Ū”÷BODĪŖµČ±ßČż½ĒŠĪ£»¢Ü”÷EOD ”× ”÷CAD£¬ÕżČ·µÄŹĒ£Ø £©
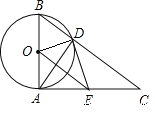
A. ¢Ł¢Ś B. ¢Ś¢Ü C. ¢Ł¢Ś¢Ü D. ¢Ł¢Ś¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDÖŠ£¬BE=EF=FC£¬CG=2GD£¬BG·Ö±š½»AE£¬AFÓŚM£¬N£®ĻĀĮŠ½įĀŪ£ŗ¢ŁAF”ĶBG£»¢ŚBN=![]() NF£»¢Ū
NF£»¢Ū![]() £»¢Ü
£»¢Ü![]() £®ĘäÖŠÕżČ·µÄ½įĀŪµÄŠņŗÅŹĒ______£®
£®ĘäÖŠÕżČ·µÄ½įĀŪµÄŠņŗÅŹĒ______£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
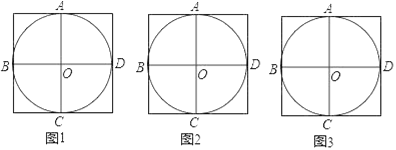
”¾ĢāÄæ”æŌŚĶ¼1”¢2ÖŠ£¬”ŃO¹żĮĖÕż·½ŠĪĶųøńÖŠµÄøńµćA”¢B”¢C”¢D£¬ĒėÄć½öÓĆĪŽæĢ¶ČµÄÖ±³ß·Ö±šŌŚĶ¼1”¢Ķ¼2”¢Ķ¼3ÖŠ»³öŅ»øöĀś×ćĻĀĮŠĢõ¼žµÄ”ĻP
£Ø1£©¶„µćPŌŚ”ŃOÉĻĒŅ²»ÓėµćA”¢B”¢C”¢DÖŲŗĻ£»
£Ø2£©”ĻPŌŚĶ¼1”¢Ķ¼2”¢Ķ¼3ÖŠµÄÕżĒŠÖµ·Ö±šĪŖ1”¢![]() ”¢2£®
”¢2£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æøł¾ŻĻĀĮŠø÷×éĢõ¼ž£¬”÷ABCÓė”÷A1B1C1ĻąĖʵÄÓŠ( )
¢Ł”ĻA£½45”ć£¬AB£½12£¬AC£½15£¬”ĻA1£½45”ć£¬A1B1£½16£¬A1C1£½20
¢ŚAB£½12£¬BC£½15£¬AC£½24£¬A1B1£½20£¬A1C1£½40£¬B1C1£½25
¢Ū”ĻB£½”ĻB1£½75”ć£¬”ĻC£½50”ć£¬”ĻA1£½55”ć
¢Ü”ĻC£½”ĻC1£½90”ć£¬AB£½10£¬AC£½6£¬A1B1£½15£¬A1C1£½9
A. 1øö B. 2øö C. 3øö D. 4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() ”¢
”¢![]() ŹĒŅŌ
ŹĒŅŌ![]() ĪŖÖ±¾¶µÄ°ėŌ²µÄĮ½ĢõĒŠĻߣ¬
ĪŖÖ±¾¶µÄ°ėŌ²µÄĮ½ĢõĒŠĻߣ¬![]() Óė°ėŌ²½»ÓŚµć
Óė°ėŌ²½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() £¬½»
£¬½»![]() ÓŚµć
ÓŚµć![]() .
.
(1)Čō»”AEµÄ¶ČŹżĪŖ140£¬Ēó![]() µÄ¶ČŹż;
µÄ¶ČŹż;
(2)ĒóÖ¤: ![]() .
.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
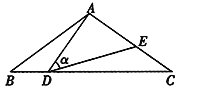
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC=10£¬µćDŹĒ±ßÉĻŅ»¶Æµć(²»ÓėB£¬CÖŲŗĻ)£¬”ĻADE=”ĻB=a£¬DE½»ACÓŚµćE£¬ĒŅcosa=![]() £¬ŌņĻ߶ĪCEµÄ×ī“óÖµĪŖ____.
£¬ŌņĻ߶ĪCEµÄ×ī“óÖµĪŖ____.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
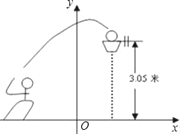
”¾ĢāÄæ”æČēĶ¼£¬Ņ»Ī»ĄŗĒņŌĖ¶ÆŌ±ĢųĘšĶ¶Ąŗ£¬ĒņŃŲÅ×ĪļĻßy=©![]() x2+3.5ŌĖŠŠ£¬Č»ŗó×¼Č·ĀäČėĄŗæņÄŚ£®ŅŃÖŖĄŗæņµÄÖŠŠÄĄėµŲĆęµÄ¾ąĄėĪŖ3.05Ć×£®
x2+3.5ŌĖŠŠ£¬Č»ŗó×¼Č·ĀäČėĄŗæņÄŚ£®ŅŃÖŖĄŗæņµÄÖŠŠÄĄėµŲĆęµÄ¾ąĄėĪŖ3.05Ć×£®
(1)ĒņŌŚæÕÖŠŌĖŠŠµÄ×ī“óø߶ČĪŖ¶ąÉŁĆ×£æ
(2)Čē¹ūøĆŌĖ¶ÆŌ±ĢųĶ¶Ź±£¬Ēņ³öŹÖĄėµŲĆęµÄø߶ČĪŖ2.25Ć×£¬ĒėĪŹĖū¾ąĄėĄŗæņÖŠŠÄµÄĖ®Ę½¾ąĄėŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
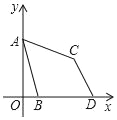
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA£Ø0£¬3£©£¬BŹĒxÖįÕż°ėÖįÉĻŅ»¶Æµć£¬½«µćAČʵćBĖ³Ź±ÕėŠż×Ŗ60”ćµĆµćC£¬OBŃÓ³¤ĻßÉĻÓŠŅ»µćD£¬Āś×ć”ĻBDC£½”ĻBAC£¬ŌņĻ߶ĪBD³¤ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com