
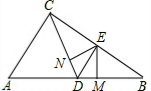
 如图,在直角△ABC中,∠ACB=90°,AC=3,BC=4,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD于M,EN⊥DC于N.
如图,在直角△ABC中,∠ACB=90°,AC=3,BC=4,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD于M,EN⊥DC于N.分析 (1)由等腰三角形的性质得出∠DAC=∠DCA,由三角形的外角性质和角平分线得出得出∠DAC=∠BDE,即可得出结论;
(2)存在以下两种情况①当∠B=∠ECN时;②当∠B=∠CNE时,根据相似三角形的性质即可求得;
(3)根据四边形MEND与△BDE的面积相等,得到△DME与△BME的面积相等.证明△BME∽△BCA,△CDE∽△CBD,即可解答.
解答 解:(1)∵AD=CD,
∴∠A=∠ACD.
∵∠CDB=∠A+∠ACD,
∴∠CDB=2∠A.
∵DE平分∠CDB,
∴∠BDE=$\frac{1}{2}$∠CDB=∠A.
∴DE∥AC.
(2)∵∠ACB=90°,AC=3,BC=4,
∴AB=5.
∵EM⊥BD,EN⊥CD,
∴∠BME=∠CNE=90°.
存在以下两种情况
①当∠B=∠ECN时,
∴CD=BD,
∵∠B+∠A=90°,∠ECN+∠ACD=90°,
∴∠A=∠ACD.
∴CD=AD.
∴AD=BD=$\frac{1}{2}$AB=$\frac{5}{2}$.
②当∠B=∠CNE时
∴NE∥AB.
∴∠ADC=∠CNE=90°.
∴∠ADC=∠ACB.
∵∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$.
∴AD=$\frac{A{C}^{2}}{AB}=\frac{9}{5}$.
综上可得:AD=$\frac{5}{2}$或$\frac{9}{5}$.
(3)∵∠EDN=∠EDM,∠DNE=∠DME=90°,DE=DE,
∴△DNE≌△DME.
∵四边形MEND与△BDE的面积相等,
∴△DME与△BME的面积相等.
∴DM=BM.
∵EM⊥BD,
∴DE=BE.
∴∠B=∠BDE=∠CDE.
∵∠B=∠B,∠BME=∠ACB=90°,
∴△BME∽△BCA.
∴$\frac{BM}{BE}=\frac{BC}{AB}=\frac{4}{5}$.
∴$\frac{BD}{BE}=\frac{8}{5}$.
∵∠DCE=∠DCB,
∴△CDE∽△CBD.
∴$\frac{BC}{CD}=\frac{CD}{CE}=\frac{BD}{DE}=\frac{BD}{BE}=\frac{8}{5}$.
∴CD=$\frac{5}{2}$.
∴CE=$\frac{25}{16}$.
∴BD=$\frac{39}{16}$.
∴BE=$\frac{39}{10}$.
∴AD=AB-BD=5-$\frac{39}{16}$=$\frac{51}{16}$.
点评 此题考查了平行线的判定,还考查了相似三角形的判定与性质,解题时要注意数形结合思想的应用,要注意不规则图形的面积的求解方法.


科目:初中数学 来源:2016-2017学年江西省下期九年级第一次月考数学试卷(解析版) 题型:单选题
如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为2a,则纸片的剩余部分的面积为( )

A. 5a B. 4a C. 3a D. 2a
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
化简(a+b+c) -(a-b+c)
-(a-b+c) 的结果为( )
的结果为( )
A. 4ab+4bc B. 4ac C. 2ac D. 4ab-4bc
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 气温(℃) | 11 | 13 | 14 | 15 | 16 |
| 天数(天) | 1 | 1 | 3 | 4 | 2 |
| A. | 三月下旬共有11天 | |
| B. | 三月下旬中,最低气温的众数是15℃ | |
| C. | 三月下旬中,最低气温的中位数是15℃ | |
| D. | 三月下旬中,最低气温的平均数是15℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A. | 70分,80分 | B. | 80分,80分 | C. | 90分,80分 | D. | 80分,90分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com