

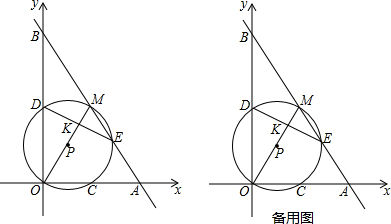
���� ��1����֤��ADE�ա�DCF������֤��AF��BE��������ϵ�ǣ�AF=BE��λ�ù�ϵ�ǣ�AF��BE��
��2��֤����ADE�ա�DCF��Ȼ��֤����ABE�ա�ADF����֤��BE=AF��Ȼ������������ڽǺͶ���֤����AMB=90�㣬�Ӷ���֤��
��3���루2���Ľⷨ��ȫ��ͬ��
��� �⣺��1��AF��BE��������ϵ�ǣ�AF=BE��λ�ù�ϵ�ǣ�AF��BE��
���ǣ���ȣ����ഹֱ��
��2��������Ȼ������
�����ǣ���������ABCD�У�AB=AD=CD��
���ڡ�ADE�͡�DCF�У�$\left\{\begin{array}{l}{AE=DF}\\{AD=CD}\\{DE=CF}\end{array}\right.$��
���ADE�ա�DCF��
���DAE=��CDF��
�֡�������ABCD�У���BAD=��ADC=90�㣬
���BAE=��ADF��
���ڡ�ABE�͡�ADF�У�$\left\{\begin{array}{l}{AB=DA}\\{��BAE=��ADF}\\{AE=DF}\end{array}\right.$��
���ABE�ա�ADF��
��BE=AF����ABM=��DAF��
�֡ߡ�DAF+��BAM=90�㣬
���ABM+��BAM=90�㣬
���ڡ�ABM�У���AMB=180��-����ABM+��BAM��=90�㣬
��BE��AF��
��3���ڣ�1�����еĽ��۶��ܳ�����
�����ǣ���������ABCD�У�AB=AD=CD��
���ڡ�ADE�͡�DCF�У�$\left\{\begin{array}{l}{AE=DF}\\{AD=CD}\\{DE=CF}\end{array}\right.$��
���ADE�ա�DCF��
���DAE=��CDF��
�֡�������ABCD�У���BAD=��ADC=90�㣬
���BAE=��ADF��
���ڡ�ABE�͡�ADF�У�$\left\{\begin{array}{l}{AB=DA}\\{��BAE=��ADF}\\{AE=DF}\end{array}\right.$��
���ABE�ա�ADF��
��BE=AF����ABM=��DAF��
�֡ߡ�DAF+��BAM=90�㣬
���ABM+��BAM=90�㣬
���ڡ�ABM�У���AMB=180��-����ABM+��BAM��=90�㣬
��BE��AF��
���� ���⿼���������κ͵ȱ������ε������Լ�ȫ�������ε��ж������ʣ�֤����BAE=��ADF�ǽ���Ĺؼ���


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
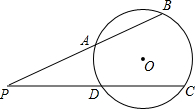 ��ͼ����O�İ뾶Ϊ5����P�ڡ�O�⣬PB����O��A��B���㣬PC����O��D��C���㣮
��ͼ����O�İ뾶Ϊ5����P�ڡ�O�⣬PB����O��A��B���㣬PC����O��D��C���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 10 | C�� | 9��10 | D�� | 8��10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
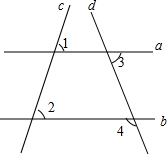 ֱ��a��b��c��d��λ����ͼ��ʾ�������1=58�㣬��2=58�㣬��3=70�㣬��ô��4���ڣ�������
ֱ��a��b��c��d��λ����ͼ��ʾ�������1=58�㣬��2=58�㣬��3=70�㣬��ô��4���ڣ�������| A�� | 58�� | B�� | 70�� | C�� | 110�� | D�� | 116�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com