练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，∠ABC=50°，∠ABD=135°，BE平分∠ABC，BE⊥BF，则∠FBD的度数为20°．

    分析 根据角平分线的定义，以及已知条件，求出∠COF的度数，进而求出∠FDB的度数．

    解答 解：∵∠ABC=50°，BE平分∠ABC，
    ∴∠CBE=$\frac{1}{2}$∠ABC=25°，
    又∵BE⊥BF，
    ∴∠CBF=∠EBF-∠EBC=90°-25°=65°，
    又∵∠ABD=135°，
    ∴∠CBD=∠ABD-∠ABC=135°-50°=85°，
    ∴∠FBD=∠CBD-∠CBF=85°-65°=20°．
    故答案为：20°．

    点评 本题考查了角平分线的定义以及垂直的定义，进而一步步计算，难度适中．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

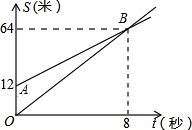    5．如图，OB，AB分别表示甲乙两名同学运动的一次函数图象，图中s与t分别表示运动路程和时间，已知甲的速度比乙快，下列说法：
    ①射线AB表示甲的路程与时间的函数关系；
    ②甲的速度比乙快1.5米/秒；
    ③甲比乙先跑12米；
    ④8秒钟后，甲超过了乙，
    其中正确的有②③④．（填写你认为所有正确的答案序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

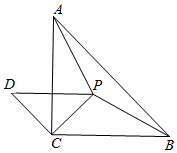    6．在等腰Rt△ABC中，∠ACB=90°，点P是△ABC内一点，且CP=$\sqrt{2}$，BP=AP=2，以点C为直角顶点，CP为直角边，作如图的等腰Rt△DCP，有如下4个结论：①点A与D的距离为2；②∠CPB=105°；③AB=$\sqrt{6}+\sqrt{2}$；④S△APB=2，其中正确的结论是（　　）
    A．①②③B．①③④C．②③④D．①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．轮船沿江从A港顺流行驶到B港，比从B港返回A港少用3小时，若船速为26千米/小时，水速为2千米/小时，设A港和B港相距x千米，则根据题意列出的方程是$\frac{x}{28}+3=\frac{x}{24}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图1，等边△ABD与等边△CBD的边长均为2，将△ABD沿AC方向向右平移k个单位到△A′B′D′的位置，得到图2，则下列说法正确的是（　　）
    ①阴影部分的周长为4；
    ②当k=$\frac{\sqrt{3}}{2}$时，图中阴影部分为正六边形；
    ③当k=$\frac{\sqrt{3}}{2}$时，图中阴影部分的面积是$\frac{5}{8}$$\sqrt{3}$．
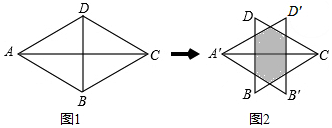
    A．①B．①②C．①③D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．比x2-4x+1少5x2-x-8的多项式是-4x2-3x+9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知|m-1|+${（\sqrt{n}-5）}^{2}$=0，则m=1，n=25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在平面直角坐标系xOy中，已知一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于点A，与y轴交于点B．
    （1）求A，B两点的坐标；
    （2）在给定的坐标系中画出该函数的图象；
    （3）点M（-1，y1），N（3，y2）在该函数的图象上，比较y1与y2的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

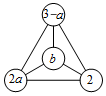    5．如图，在一个三角形三个顶点和中心处的每个“○”中各填有一个式子，如果图中任意三个“○”中的式子之和均相等，那么a的值为（　　）
    A．1B．2C．3D．0

    查看答案和解析>>

    同步练习册答案