
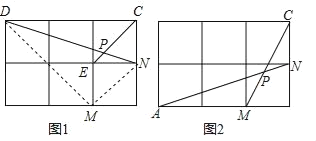
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OC=6,D是半径OC上一点,且 OD=4.A,B是⊙O上的两个动点,∠ADB=90°,F是AB的中点,则OF的长的最大值等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
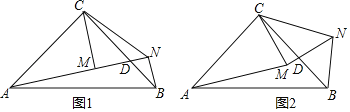
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,以C为顶点作等腰直角三角形CMN.使∠CMN=90°,连接BN,射线NM交BC于点D.
(1)如图1,若点A,M,N在一条直线上,
①求证:BN+CM=AM;
②若AM=4,BN=![]() ,求BD的长;
,求BD的长;
(2)如图2,若AB=4,CN=2,将△CMN绕点C顺时针旋转一周,在旋转过程中射线NM交AB于点H,当三角形DBH是直角三角形时,请你直接写出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生准备购买标价为50元的《现代汉语词典》,现有甲、乙两书店出售此书,甲店按如下方法促销:若只购1本,则按原价销售;若一次性购买多于1本,但不多于30本时,每多购一本,售价在标价的基础上优惠2%(例如买2本,每本售价优惠2%;买三本,每本售价优惠4%,以此类推);若多于30本,每本售价20元.乙书店一律按标价的6折销售.
(1)分别写出在两书店购买此书总价y甲、y乙与购书本数x之间的函数关系式;
(2)若这些学生一次性购买多于30本时,那么去哪家书店购买更划算,为什么?若要一次性购买不多于30本时,先写出y(y=y甲﹣y乙)与购买本数x之间的函数式,画出其图象,再利用函数图象分析去哪家书店购买更划算.

查看答案和解析>>
科目:初中数学 来源: 题型:
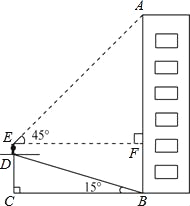
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数, ![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
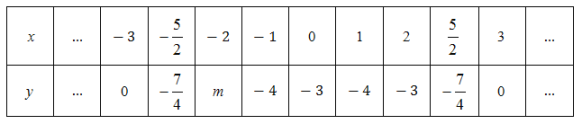
其中,![]() ________.
________.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
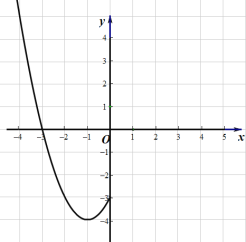
(3)观察函数![]() 图象,回答下列问题:
图象,回答下列问题:
①函数图像的对称性是: .
②当![]() 时,写出
时,写出![]() 随
随![]() 的变化规律: .
的变化规律: .
(4)进一步探究函数图象发现:方程![]() 有________个实数根.
有________个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
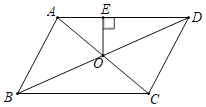
【题目】如图,□ABCD的对角线AC与BD相交于点O,过点O作OE⊥AD于点E,若AB=4,∠ABC=60°,则OE的长是( )
A.![]() B.2
B.2![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AO=BO=50cm,OC是一条射线,OC⊥AB,一只蚂蚁由A以2cm/s的速度向B爬行;同时另一只蚂蚁由O点以3cm/s的速度沿OC方向爬行.问:是否存在这样的时刻,使两只小蚂蚁与点O点组成的三角形面积为450cm2?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com