
���� ���Ƿ�ʽ�ķ�ĸ��Ϊ0������ʽ���������壻
��1����ʾ����ʽ���̵Ľ⣬�ɽ�Ϊ����ȷ����m�ķ�Χ���ɣ�
��2����ʽ����ȥ��ĸת��Ϊ��ʽ���̣����ݷ�ʽ�����⣬�õ�����������ʽ�����⣬ȷ����n�ķ�Χ���ɣ�
��� �⣺��ش�С��û�п��Ƿ�ʽ�ķ�ĸ��Ϊ0�����ʽ���������壩���������
��1�������x�ķ�ʽ���̵ã�x=$\frac{3}{2m-1}$��
�߷����н⣬�ҽ�Ϊ������
��$\left\{\begin{array}{l}2m-1��0\\ \frac{3}{2m-1}��-2\end{array}\right.$��
��ã�m��$\frac{1}{2}$��m��-$\frac{1}{4}$��
��2����ʽ����ȥ��ĸ�ã�3-2x+nx-2=-x+3������n-1��x=2��
�ɷ�ʽ�����⣬�õ�x-3=0����x=3��
������ʽ���̵ã�n=$\frac{5}{3}$��
��n-1=0ʱ����ʽ�����⣬��ʱn=1��
���ϣ�n=1��n=$\frac{5}{3}$��
���� ���⿼���˽��ʽ���̣�������ת����˼�룬���ʽ����ע��Ҫ���飮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
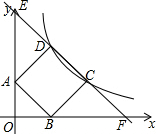 ��ͼ��������ABCD�У���A��B���������ϣ�C��D�ڵ�һ�����ڣ�����������y=$\frac{k}{x}$��ͼ��D��1��2����C�㣮
��ͼ��������ABCD�У���A��B���������ϣ�C��D�ڵ�һ�����ڣ�����������y=$\frac{k}{x}$��ͼ��D��1��2����C�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
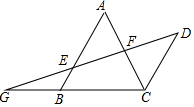 ��ͼ����ABC�У�AB=BC=4��CD��AB����D���ֱ�߽�AC��AB�ڵ�F��E����CB���ӳ����ڵ�G��DF=EF��
��ͼ����ABC�У�AB=BC=4��CD��AB����D���ֱ�߽�AC��AB�ڵ�F��E����CB���ӳ����ڵ�G��DF=EF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
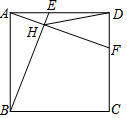 ��ͼ��������ABCD�ı�AD��CD����������E��F��������AF=BE��BE��AF�ڵ�H���������εı߳�Ϊ4���߶�DH���ֵΪx����СֵΪy����$\sqrt{x}$-y��ֵ��4-2$\sqrt{5}$��
��ͼ��������ABCD�ı�AD��CD����������E��F��������AF=BE��BE��AF�ڵ�H���������εı߳�Ϊ4���߶�DH���ֵΪx����СֵΪy����$\sqrt{x}$-y��ֵ��4-2$\sqrt{5}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com