练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下面四个图形中，既是中心对称图形又是轴对称图形的是（ ）
    A.
    B.
    C.
    D.

    【答案】B
    【解析】解：A、是轴对称图形，不是中心对称图形，不合题意；

    B、是轴对称图形，也是中心对称图形，符合题意；

    C、不是轴对称图形，是中心对称图形，不合题意；

    D、是轴对称图形，不是中心对称图形，不合题意．

    所以答案是：B．

    【考点精析】本题主要考查了轴对称图形和中心对称及中心对称图形的相关知识点，需要掌握两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴；如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，两块直角三角板的直角顶点O重合在一起，若∠BOC＝∠AOD，则∠BOC的度数为（　　）

    A.22.5°B.30°C.45°D.60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解全校2400名学生的阅读兴趣，从中随机抽查了部分同学，就“我最感兴趣的书籍”进行了调查：A.小说、B.散文、C.科普、D.其他（每个同学只能选择一项），进行了相关统计，整理并绘制出两幅不完整的统计图，请你根据统计图提供的信息，解答下列问题：

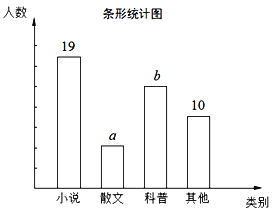
    （1）本次抽查中，样本容量为______；

    （2）a＝______，b＝______；

    （3）扇形统计图中，其他类书籍所在扇形的圆心角是______°；

    （4）请根据样本数据，估计全校有多少名学生对散文感兴趣．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场计划用3 800元购进节能灯120只，这两种节能灯的进价、售价如下表：

    进价(元/只)

    售价(元/只)

    甲型

    25

    30

    乙型

    45

    60

    (1)求甲、乙两种节能灯各进多少只？

    (2)全部售完120只节能灯后，该商场获利润多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校计划购买甲、乙两种图书作为“校园读书节”的奖品，已知甲种图书的单价比乙种图书的单价多10元，且购买3本甲种图书和2本乙种图书共需花费130元

    (1)甲、乙两种图书的单价分别为多少元？

    (2)学校计划购买这两种图书共50本，且投入总经费不超过1200元，则最多可以购买甲种图书多少本？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算或化简:

    （1）；

    （）；

    （3）；

    （4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某农场有A、B两种型号的收割机共20台，每台A型收割机每天可收大麦100亩或者小麦80亩，每台B型收割机每天可收大麦80亩或者小麦60亩，该农场现有19 000亩大麦和11 500亩小麦先后等待收割．先安排这20台收割机全部收割大麦，并且恰好10天时间全部收完.

    （1）问A、B两种型号的收割机各多少台？

    （2）由于气候影响，要求通过加班方式使每台收割机每天多完成10%的收割量，问这20台收割机能否在一周时间内完成全部小麦收割任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在矩形ABCD中，AB=4cm，AD=6cm，延长AB到E，使BE=2AB，连接CE，动点F从A出发以2cm/s的速度沿AE方向向点E运动，动点G从E点出发，以3cm/s的速度沿E→C→D方向向点D运动，两个动点同时出发，当其中一个动点到达终点时，另一个动点也随之停止，设动点运动的时间为t秒．

    （1）当t为何值时，FC与EG互相平分；
    （2）连接FG，当t＜ 时，是否存在时间t使△EFG与△EBC相似？若存在，求出t的值；若不存在，请说明理由．
    （3）设△EFG的面积为y，求出y与t的函数关系式，求当t为何值时，y有最大值？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：以O为圆心的扇形AOB中，∠AOB=90°，点C为 上一动点，射线AC交射线OB于点D，过点D作OD的垂线交射线OC于点E，联结AE．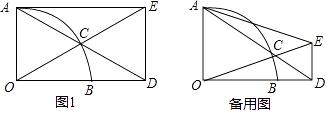

    （1）如图1，当四边形AODE为矩形时，求∠ADO的度数；
    （2）当扇形的半径长为5，且AC=6时，求线段DE的长；
    （3）联结BC，试问：在点C运动的过程中，∠BCD的大小是否确定？若是，请求出它的度数；若不是，请说明理由．

    查看答案和解析>>

    同步练习册答案