
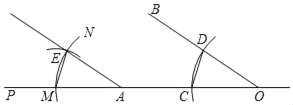
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。

证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
【答案】对顶角相等;DMN;同位角相等,两直线平行;同旁内角互补;已知;∠D;同旁内角互补;
两直线平行 ,内错角相等.
【解析】试题分析:由∠1=∠2,∠1=∠DMN,根据同位角相等,两直线平行,易证得DB∥EC,又由∠C=∠D,易证得AC∥DF,继而证得结论.
试题解析:证明:∵∠1=∠2(已知),
又∠1=∠DMN(_对顶角相等),
∴∠2=∠_DMN_(等量代换),
∴DB∥EC( 同位角相等,两直线平行 ),
∴∠DBC+∠C=1800(两直线平行 , 同旁内角互补 ),
∵∠C=∠D( 已知 ),
∴∠DBC+ ∠D =1800(等量代换),
∴DF∥AC( 同旁内角互补 ,两直线平行),
∴∠A=∠F( 两直线平行 ,内错角相等 )
故答案为:对顶角相等;DMN,同位角相等,两直线平行;∠ABD=∠C;两直线平行,同位角相等;∠ABD=∠D;等量代换;内错角相等,两直线平行;(两直线平行,内错角相等).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是_____米,小明在书店停留了_____分钟;
(2)本次上学途中,小明一共行驶了______米,一共用了_____分钟;
(3)在整个上学的途中______(哪个时间段)小明骑车速度最快,最快的速度是____米/分;
(4)小明出发多长时间离家1200米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店在某一时间以每件a元(a>0)的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%.
(1)当a=60时,分析卖出这两件衣服总的是盈利还是亏损,或是不盈不亏?
(2)小安发现:不论a为何值,这样卖两件衣服总的都是亏损.请判断“小安发现”是否正确?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOP与OP上点C,点A(在A的左侧),嘉嘉进行如下作图:
①以点O为圆心,OC为半径画弧,交OB于点D,连接CD
②以点A为圆心,OC为半径画弧MN,交AP于点M
③以点M为圆心,CD为半径画弧,交MN于点E,连接ME,作射线AE
如图所示,则下列结论不成立的是( )
A. CD∥EM B. AE∥OB C. ∠ODC=∠AEM D. ∠OAE=∠BDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.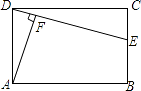
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角” (如图)就是一例.这个三角形给出了![]() (n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着
展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着![]() 展开式中各项的系数,等等.
展开式中各项的系数,等等.

有如下三个结论:
①当a=1,b=1时,代数式![]() 的值是1;
的值是1;
②当a=-1,b=2时,代数式![]() 的值是1;
的值是1;
③当代数式![]() 的值是1时,a的值是-2或-4.
的值是1时,a的值是-2或-4.
上述结论中,所有正确结论的序号为( )
A. ①② B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点A出发,沿AB方向匀速运动,速度为1cm/s;过点P作直线PF∥AD,PF交CD于点F,过点F作EF⊥BD,且与AD、BD分别交于点E、Q;连接PE,设点P的运动时间为t(s)(0<t<10).![]() 解答下列问题:
解答下列问题:
(1)填空:AB= cm;
(2)当t为何值时,PE∥BD;
(3)设四边形APFE的面积为y(cm2)
①求y与t之间的函数关系式;
②若用S表示图形的面积,则是否存在某一时刻t,使得S四边形APFE= ![]() S菱形ABCD?若存在,求出t的值;若不存在,请说明理由.
S菱形ABCD?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若 ![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬买了A、B两种书,单价分别是18元、10元.
(1)若两种书共买了10本付款172元,求每种书各买了多少本?
(2)买10本时付款可能是123元吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com