
 如图,两个边长相等的正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,则两个正方形的重叠部分四边形OMCN的面积( )
如图,两个边长相等的正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,则两个正方形的重叠部分四边形OMCN的面积( )| 1 |
| 4 |
|
| 1 |
| 4 |
| 1 |
| 4 |


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
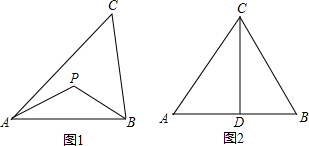
用两个边长为![]() 的全等的等边
的全等的等边![]() 与
与![]() 拼成一个四边形
拼成一个四边形![]() ,把一个含
,把一个含![]() 角的直角三角尺与此四边形重合,使三角尺的
角的直角三角尺与此四边形重合,使三角尺的![]() 角的顶点与点
角的顶点与点![]() 重合,两边分别与
重合,两边分别与![]() 、
、![]() 重合. 将三角尺绕点
重合. 将三角尺绕点![]() 按逆时针方向旋转(旋转角小于
按逆时针方向旋转(旋转角小于![]() ).
).
(1)当三角尺的两边分别与四边形![]() 的两边
的两边![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 时,如图(1),①求证:1).∠BAE=∠CAF,2).
时,如图(1),①求证:1).∠BAE=∠CAF,2).![]() ;②重叠部分(四边形
;②重叠部分(四边形![]() )的面积为 .
)的面积为 .
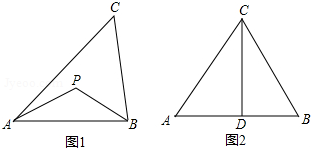
(2)当三角尺的两边分别与四边形![]() 的两边
的两边![]() 、
、![]() 的延长线相交于点
的延长线相交于点![]() 、
、![]() 时,如图(2),①
时,如图(2),①![]() 还相等吗?说明理由;
还相等吗?说明理由;
②重叠部分的面积 (填“改变”或“不变”)
(3)若重叠部分面积保持不变,则旋转角![]() 的取值范围是 .
的取值范围是 .
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com