
”¾ĢāÄæ”æŅŃÖŖµćA£Ø©1£¬2£©”¢B£Ø3£¬6£©ŌŚÅ×ĪļĻßy=ax2+bxÉĻ
(1)ĒóÅ×ĪļĻߵĽāĪöŹ½£»
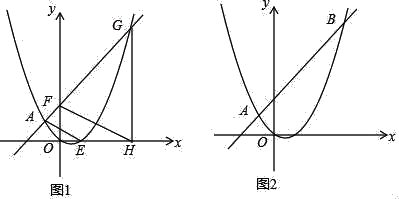
(2)ČēĶ¼1£¬µćFµÄ×ų±źĪŖ£Ø0£¬m£©£Øm£¾2£©£¬Ö±ĻßAF½»Å×ĪļĻßÓŚĮķŅ»µćG£¬¹żµćG×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖH£®ÉčÅ×ĪļĻßÓėxÖįµÄÕż°ėÖį½»ÓŚµćE£¬Į¬½ÓFH”¢AE£¬ĒóÖ¤£ŗFH”ĪAE£»
(3)ČēĶ¼2£¬Ö±ĻßAB·Ö±š½»xÖį”¢yÖįÓŚC”¢DĮ½µć£®µćP“ÓµćC³ö·¢£¬ŃŲÉäĻßCD·½ĻņŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖĆæĆė![]() øöµ„Ī»³¤¶Č£»Ķ¬Ź±µćQ“ÓŌµćO³ö·¢£¬ŃŲxÖįÕż·½ĻņŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖĆæĆė1øöµ„Ī»³¤¶Č£®µćMŹĒÖ±ĻßPQÓėÅ×ĪļĻßµÄŅ»øö½»µć£¬µ±ŌĖ¶Æµ½tĆėŹ±£¬QM=2PM£¬Ö±½ÓŠ“³ötµÄÖµ£®
øöµ„Ī»³¤¶Č£»Ķ¬Ź±µćQ“ÓŌµćO³ö·¢£¬ŃŲxÖįÕż·½ĻņŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖĆæĆė1øöµ„Ī»³¤¶Č£®µćMŹĒÖ±ĻßPQÓėÅ×ĪļĻßµÄŅ»øö½»µć£¬µ±ŌĖ¶Æµ½tĆėŹ±£¬QM=2PM£¬Ö±½ÓŠ“³ötµÄÖµ£®
”¾“š°ø”æ(1)Å×ĪļĻߵĽāĪöŹ½ĪŖy=x2©x£»(2)Ö¤Ć÷¼ū½āĪö£»(3)µ±ŌĖ¶ÆŹ±¼äĪŖ![]() »ņ
»ņ![]() ĆėŹ±£¬QM=2PM£®
ĆėŹ±£¬QM=2PM£®
”¾½āĪö”æ
£Ø1£©£Ø1£©A£¬BµÄ×ų±ź“śČėÅ×ĪļĻßy=ax2+bxÖŠČ·¶Ø½āĪöŹ½£»
£Ø2£©°ŃAµć×ų±ź“śČėĖłÉčµÄAFµÄ½āĪöŹ½£¬ÓėÅ×ĪļĻߵĽāĪöŹ½¹¹³É·½³Ģ×飬½āµĆGµć×ų±ź£¬ŌŁĶعżÖ¤Ć÷Čż½ĒŠĪĻąĖĘ£¬µĆµ½Ķ¬Ī»½ĒĻąµČ£¬Į½Ö±ĻßĘ½ŠŠ£»
£Ø3£©¾ßĢå¼ūĻź½ā.
£®½ā£ŗ£Ø1£©½«µćA£Ø©1£¬2£©”¢B£Ø3£¬6£©“śČėÖŠ£¬
![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬
£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=x2©x£®
£Ø2£©Ö¤Ć÷£ŗÉčÖ±ĻßAFµÄ½āĪöŹ½ĪŖy=kx+m£¬
½«µćA£Ø©1£¬2£©“śČėy=kx+mÖŠ£¬¼“©k+m=2£¬
”ąk=m©2£¬
”ąÖ±ĻßAFµÄ½āĪöŹ½ĪŖy=£Øm©2£©x+m£®
ĮŖĮ¢Ö±ĻßAFŗĶÅ×ĪļĻß½āĪöŹ½³É·½³Ģ×飬
![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() »ņ
»ņ![]() £¬
£¬
”ąµćGµÄ×ų±źĪŖ£Øm£¬m2©m£©£®
”ßGH”ĶxÖį£¬
”ąµćHµÄ×ų±źĪŖ£Øm£¬0£©£®
”ßÅ×ĪļĻߵĽāĪöŹ½ĪŖy=x2©x=x£Øx©1£©£¬
”ąµćEµÄ×ų±źĪŖ£Ø1£¬0£©£®
¹żµćA×÷AA”ä”ĶxÖį£¬“¹×ćĪŖµćA”䣬ČēĶ¼1ĖłŹ¾£®
”ßµćA£Ø©1£¬2£©£¬
”ąA”ä£Ø©1£¬0£©£¬
”ąAE=2£¬AA”ä=2£®
”ą![]() =1£¬
=1£¬![]() =
=![]() =1£¬
=1£¬
”ą![]() =
= ![]() £¬
£¬
”ß”ĻAA”äE=”ĻFOH£¬
”ą”÷AA”äE”×”÷FOH£¬
”ą”ĻAEA”ä=”ĻFHO£¬
”ąFH”ĪAE£®
£Ø3£©ÉčÖ±ĻßABµÄ½āĪöŹ½ĪŖy=k0x+b0£¬
½«A£Ø©1£¬2£©”¢B£Ø3£¬6£©“śČėy=k0x+b0ÖŠ£¬µĆ ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬
£¬
”ąÖ±ĻßABµÄ½āĪöŹ½ĪŖy=x+3£¬
µ±ŌĖ¶ÆŹ±¼äĪŖtĆėŹ±£¬µćPµÄ×ų±źĪŖ£Øt©3£¬t£©£¬µćQµÄ×ų±źĪŖ£Øt£¬0£©£®
µ±µćMŌŚĻ߶ĪPQÉĻŹ±£¬¹żµćP×÷PP”ä”ĶxÖįÓŚµćP”䣬¹żµćM×÷MM”ä”ĶxÖįÓŚµćM”䣬Ōņ”÷PQP”ä”×”÷MQM”䣬ČēĶ¼2ĖłŹ¾£¬
”ßQM=2PM£¬
”ą![]() =
=![]() £¬
£¬
”ąQM”ä=![]() QP'=2£¬MM”ä=
QP'=2£¬MM”ä=![]() PP'=
PP'=![]() t£¬
t£¬
”ąµćMµÄ×ų±źĪŖ£Øt©2£¬![]() t£©£®
t£©£®
Ó֔ߵćMŌŚÅ×ĪļĻßy=x2©xÉĻ£¬
”ą![]() t=£Øt©2£©2©£Øt©2£©£¬
t=£Øt©2£©2©£Øt©2£©£¬
½āµĆ£ŗt=![]() £»
£»
µ±µćMŌŚĻ߶ĪQPµÄŃÓ³¤ĻßÉĻŹ±£¬
Ķ¬ĄķæÉµĆ³öµćMµÄ×ų±źĪŖ£Øt©6£¬2t£©£¬
”ßµćMŌŚÅ×ĪļĻßy=x2©xÉĻ£¬
”ą2t=£Øt©6£©2©£Øt©6£©£¬
½āµĆ£ŗt=![]() £®
£®
×ŪÉĻĖłŹö£ŗµ±ŌĖ¶ÆŹ±¼äĆė![]() »ņ
»ņ![]() Ź±£¬QM=2PM£®
Ź±£¬QM=2PM£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĪÄ»ÆÓĆĘ·ÉĢµźÓĆ2000ŌŖ¹ŗ½ųŅ»ÅśŃ§ÉśŹé°ü£¬Ćꏊŗó·¢ĻÖ¹©²»Ó¦Ēó£¬ÉĢµźÓÖ¹ŗ½ųµŚ¶žÅśĶ¬ŃłµÄŹé°ü£¬Ėł¹ŗŹżĮæŹĒµŚŅ»Åś¹ŗ½ųŹżĮæµÄ3±¶£¬µ«µ„¼Ū¹óĮĖ4ŌŖ£¬½į¹ūµŚ¶žÅśÓĆĮĖ6300ŌŖ”£
£Ø1£©ĒóµŚŅ»Åś¹ŗ½ųŹé°üµÄµ„¼ŪŹĒ¶ąÉŁŌŖ£æ
£Ø2£©ČōÉĢµźĻśŹŪÕāĮ½ÅśŹé°üŹ±£¬ĆæøöŹŪ¼Ū¶¼ŹĒ120ŌŖ£¬Č«²æŹŪ³öŗó£¬ÉĢµź¹²ÓÆĄū¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
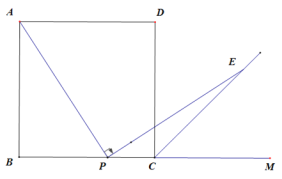
”¾ĢāÄæ”æČēĶ¼£¬µćPŹĒÕż·½ŠĪABCDµÄ±ßBCÉĻŅ»µć£¬µćMŌŚBCµÄŃÓ³¤ĻßÉĻ£¬ČōAP=PEĒŅ”ĻAPEĪŖÖ±½Ē£®ĒóÖ¤£ŗCEĘ½·Ö”ĻDCM£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() ÓŚµć
ÓŚµć![]() £¬
£¬![]() ŗĶ
ŗĶ![]() µÄ½ĒĘ½·ÖĻßĻą½»ÓŚµć
µÄ½ĒĘ½·ÖĻßĻą½»ÓŚµć![]() £¬
£¬![]() ĪŖ±ß
ĪŖ±ß![]() µÄÖŠµć£¬
µÄÖŠµć£¬![]() £¬Ōņ
£¬Ōņ![]() £Ø £©
£Ø £©

A.125”ćB.145”ćC.175”ćD.190”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼Ļó¾¹żµć£Ø©1£¬2£©£¬ĒŅÓėxÖį½»µćµÄŗį×ų±źĪŖx1”¢x2£¬ĘäÖŠ©2£¼x1£¼©1”¢0£¼x2£¼1ĻĀĮŠ½įĀŪ£ŗ¢Ł4a©2b+c£¼0¢Ś2a©b£¼0¢Ūabc£¾0¢Üb2+8a£¾4acÕżČ·µÄ½įĀŪŹĒ_____£®
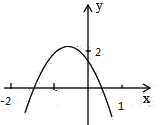
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
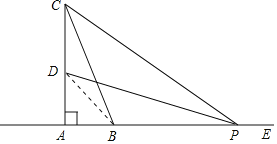
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC£½90”ć£¬AB£½5cm£¬BC£½13cm£¬µćDŌŚĻ߶ĪACÉĻ£¬ĒŅCD£½7cm£¬¶ÆµćP“Ó¾ąBµć15cmµÄEµć³ö·¢£¬ŅŌĆæĆė2cmµÄĖŁ¶ČŃŲÉäĻßEAµÄ·½ĻņŌĖ¶Æ£¬Ź±¼äĪŖtĆė£®
£Ø1£©ĒóADµÄ³¤£®
£Ø2£©ÓĆŗ¬ÓŠtµÄ“śŹżŹ½±ķŹ¾APµÄ³¤£®
£Ø3£©ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³øöŹ±æĢ£¬Ź¹”÷ABCÓė”÷ADPČ«µČ£æČō“ęŌŚ£¬ĒėĒó³ötÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø4£©Ö±½ÓŠ“³öt£½______ĆėŹ±£¬”÷PBCĪŖµČŃüČż½ĒŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
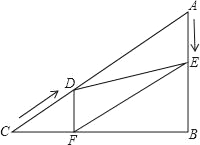
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻB£½90”ć£¬AC£½60cm£¬”ĻA£½60”ć£¬µćD“ÓµćC³ö·¢ŃŲCA·½ĻņŅŌ4cm/sµÄĖŁ¶ČĻņµćAŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±µćE“ÓµćA³ö·¢ŃŲAB·½ĻņŅŌ2cm/sµÄĖŁ¶ČĻņµćBŌČĖŁŌĖ¶Æ£¬µ±ĘäÖŠŅ»øöµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®ÉčµćD£¬EŌĖ¶ÆµÄŹ±¼äŹĒts£Ø0£¼t”Ü15£©£®¹żµćD×÷DF”ĶBCÓŚµćF£¬Į¬½ÓDE£¬EF£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪAEFDŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©µ±tĪŖŗĪÖµŹ±£¬”÷DEFĪŖÖ±½ĒČż½ĒŠĪ£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
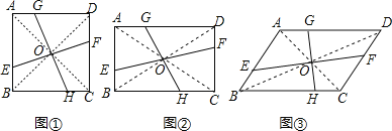
”¾ĢāÄæ”æŌŚĖıߊĪABCDÖŠ£¬¶Ō½ĒĻßAC”¢BDĻą½»ÓŚµćO£¬¹żµćOµÄÖ±Ļß·Ö±š½»±ßAB”¢CD”¢AD”¢BCÓŚµćE”¢F”¢G”¢H
£ØøŠÖŖ£©ČēĶ¼¢Ł£¬ČōĖıߊĪABCDŹĒÕż·½ŠĪ£¬ĒŅEF”ĶGH£¬Ņ×ÖŖS”÷BOE=S”÷AOG£¬ÓÖŅņĪŖS”÷AOB=![]() SĖıߊĪABCD£¬ĖłŅŌSĖıߊĪAEOG=
SĖıߊĪABCD£¬ĖłŅŌSĖıߊĪAEOG=![]() SÕż·½ŠĪABCD£Ø²»ŅŖĒóÖ¤Ć÷£©£»
SÕż·½ŠĪABCD£Ø²»ŅŖĒóÖ¤Ć÷£©£»
£ØĶŲÕ¹£©ČēĶ¼¢Ś£¬ČōĖıߊĪABCDŹĒ¾ŲŠĪ£¬ĒŅSĖıߊĪAEOG=![]() S¾ŲŠĪABCD£¬ČōAB=a£¬AD=b£¬BE=m£¬ĒóAGµÄ³¤£ØÓĆŗ¬a”¢b”¢mµÄ“śŹżŹ½±ķŹ¾£©£»
S¾ŲŠĪABCD£¬ČōAB=a£¬AD=b£¬BE=m£¬ĒóAGµÄ³¤£ØÓĆŗ¬a”¢b”¢mµÄ“śŹżŹ½±ķŹ¾£©£»
£ØĢ½¾æ£©ČēĶ¼¢Ū£¬ČōĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬ĒŅSĖıߊĪAEOG=![]() SABCD£¬ČōAB=3£¬AD=5£¬BE=1£¬ŌņAG=______£®
SABCD£¬ČōAB=3£¬AD=5£¬BE=1£¬ŌņAG=______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔ĆōĖ¼æ¼½ā¾öČēĻĀĪŹĢā£ŗ
ŌĢā£ŗČēĶ¼1£¬ĖıߊĪABCDÖŠ![]() £¬
£¬![]() £¬
£¬![]() µćP£¬Q·Ö±šŌŚĖıߊĪABCDµÄ±ßBC£¬CDÉĻ£¬
µćP£¬Q·Ö±šŌŚĖıߊĪABCDµÄ±ßBC£¬CDÉĻ£¬![]() £¬ĒóÖ¤£ŗ
£¬ĒóÖ¤£ŗ![]() £®
£®
![]() ______£»
______£»
![]() Š”Ćō½ųŠŠĢ½Ė÷£¬ČēĶ¼2£¬½«µćP£¬QµÄĪ»ÖĆĢŲŹā»Æ£¬Ź¹
Š”Ćō½ųŠŠĢ½Ė÷£¬ČēĶ¼2£¬½«µćP£¬QµÄĪ»ÖĆĢŲŹā»Æ£¬Ź¹![]() £¬
£¬![]() £¬µćE£¬F·Ö±šŌŚ±ßBC£¬CDÉĻ£¬“ĖŹ±ĖżÖ¤Ć÷ĮĖ
£¬µćE£¬F·Ö±šŌŚ±ßBC£¬CDÉĻ£¬“ĖŹ±ĖżÖ¤Ć÷ĮĖ![]() ĒėÄćÖ¤Ć÷“ĖŹ±½įĀŪ£»
ĒėÄćÖ¤Ć÷“ĖŹ±½įĀŪ£»
![]() ŹÜŅŌÉĻ
ŹÜŅŌÉĻ![]() µÄĘō·¢£¬ŌŚŌĢāÖŠ£¬Ģķ¼ÓøØÖśĻߣŗČēĶ¼3£¬×÷
µÄĘō·¢£¬ŌŚŌĢāÖŠ£¬Ģķ¼ÓøØÖśĻߣŗČēĶ¼3£¬×÷![]() £¬
£¬![]() £¬“¹×ć·Ö±šĪŖE£¬F£¬ĒėÄć¼ĢŠųĶź³ÉŌĢāµÄÖ¤Ć÷£®
£¬“¹×ć·Ö±šĪŖE£¬F£¬ĒėÄć¼ĢŠųĶź³ÉŌĢāµÄÖ¤Ć÷£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com