
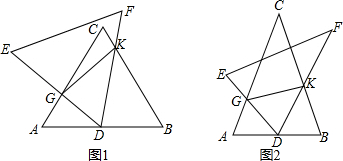
���� ��1���ɵȱ������ε����ʵó���A=��B=��EDF=60�㣬���������ε�������ʵó���AGD=��BDK��֤����DAG�ס�KBD���ó���Ӧ�߳ɱ���$\frac{AD}{BK}=\frac{DG}{DK}$��֤��AD=BD=2���ó�$\frac{BD}{BK}=\frac{DG}{DK}$��֤����KDG�ס�KDB���ɣ�
��2���ɵȱ������ε����ʵó���A=��B=��EDF=60�㣬���������ε�������ʵó���AGD=��BDK��֤����DAG�ס�KBD���ó���Ӧ�߳ɱ���$\frac{AD}{BK}=\frac{DG}{DK}$��֤��AD=BD=2���ó�$\frac{BD}{BK}=\frac{DG}{DK}$��֤����KDG�ס�KDB�����ɵó����ۣ�
��3���ɵ��������ε����ʵó���A=��B=��EDF�����������ε�������ʵó���AGD=��BDK��֤����DAG�ס�KBD���ó���Ӧ�߳ɱ���$\frac{AD}{BK}=\frac{DG}{DK}$��֤��AD=BD=2���ó�$\frac{BD}{BK}=\frac{DG}{DK}$��֤����KDG�ס�KDB��֤����DAG�ס�KDG���ó�DG•DK=2x����DKG�����S=$\frac{1}{2}$DG•DK•sin��EDF�����ɵó��������KG��ABʱ��KG��С=$\frac{1}{2}$AB=2����K��C�غ�ʱ��KG���=3�����ɵó�x��ȡֵ��Χ��
��4���ⷨͬ��1����2����
��� ��1���⣺��DAG�ס�KBD����KDG�ס�KDB���������£�
���ߡ�ABC�͡�DEF������ȫ�ȵĵȱ������Σ�
���A=��B=��EDF=60�㣬
�ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF��
���AGD=��BDK��
���DAG�ס�KBD��
��$\frac{AD}{BK}=\frac{DG}{DK}$��
�ߵ�D��AB���е㣬
��AD=BD=2��
��$\frac{BD}{BK}=\frac{DG}{DK}$��
���KDG�ס�KDB��
��2��֤�����ߡ�ABC�͡�DEF������ȫ�ȵĵȱ������Σ�
���A=��B=��EDF=60�㣬
�ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF��
���AGD=��BDK��
���DAG�ס�KBD��
��$\frac{AD}{BK}=\frac{DG}{DK}$��
�ߵ�D��AB���е㣬
��AD=BD=2��
��$\frac{BD}{BK}=\frac{DG}{DK}$��
���KDG�ס�KDB��
���GKD=��BKD��
��3���⣺�ɣ�2���ã���DAG�ס�KBD����KDG�ס�KDB��
���DAG�ס�KDG��
��$\frac{DG}{KG}=\frac{AD}{DK}$����$\frac{DG}{x}=\frac{2}{DK}$��
��DG•DK=2x��
���DKG�����S=$\frac{1}{2}$DG•DK•sin��EDF=$\frac{1}{2}$•2x•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$x��
��KG��ABʱ��KG��С=$\frac{1}{2}$AB=2����K��C�غ�ʱ��KG���=3��
��S=$\frac{\sqrt{3}}{2}$x��2��x��3����
��4���⣺��1����2���еĽ�����Ȼ�������������£�
�ߡ�ABC�͡�DEF������ȫ�ȵĵ��������Σ�DF=EF=AC=BC��
���A=��B=��EDF��
�ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF��
���AGD=��BDK��
���DAG�ס�KBD��
��$\frac{AD}{BK}=\frac{DG}{DK}$��
�ߵ�D��AB���е㣬
��AD=BD=2��
��$\frac{BD}{BK}=\frac{DG}{DK}$��
���KDG�ס�KDB��
���GKD=��BKD��
���� �������������ۺ���Ŀ�����������������ε��ж������ʡ��ȱ������ε����ʡ����������ε����ʡ������ε�������ʵ�֪ʶ�������ۺ���ǿ����һ���Ѷȣ�֤�������������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com