
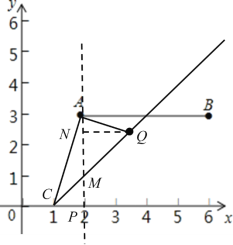
【题目】如图,在平面直角坐标系中,已知点![]() 、
、![]() ,连接
,连接![]() .如果点
.如果点![]() 在直线
在直线![]() 上,且点
上,且点![]() 到直线
到直线![]() 的距离不大于1,那么称点
的距离不大于1,那么称点![]() 是线段
是线段![]() 的“临近点”.
的“临近点”.

(1)判断点![]() 是否是线段
是否是线段![]() 的“临近点”,并说明理由;
的“临近点”,并说明理由;
(2)若点![]() 是线段
是线段![]() 的“临近点”.①求
的“临近点”.①求![]() 的取值范围;②设直线
的取值范围;②设直线![]() 与
与![]() 轴交于
轴交于![]() 点,试用
点,试用![]() 表达
表达![]() 的面积
的面积![]() ,并求出
,并求出![]() 的最大面积.
的最大面积.
【答案】(1)是,见解析;(2)①3≤m≤5;②S=m-1;最大面积为4
【解析】
(1)把C代入y=x-1中检验,求出C到直线AB的距离,即可作出判断;
(2)①根据题意列出关于m的不等式,求出解集即可确定出m的范围;
②过A作AP⊥x轴于点P,交直线CQ于点M,过点Q作QN⊥AP于点N,求出M、N、P的坐标,利用S=![]() 表示出△ACQ的面积,再根据m的取值范围得出S的最大值.
表示出△ACQ的面积,再根据m的取值范围得出S的最大值.
解:(1)把x=![]() 代入y=x-1得:y=
代入y=x-1得:y=![]() -1=
-1=![]() ,即C在直线y=x-1上,
,即C在直线y=x-1上,
∵C到线段AB的距离d=3-![]() =
=![]() <1,
<1,
∴点![]() 是线段AB的“邻近点”;
是线段AB的“邻近点”;
(2)①若点Q(m,n)是线段AB的“邻近点”,则有n=m-1,且|n-3|≤1,
∴|m-4|≤1,即-1≤m-4≤1,
解得:3≤m≤5;
②如图,过A作AP⊥x轴于点P,交直线CQ于点M,过点Q作QN⊥AP于点N,
∵A(2,3),
在![]() 中,令y=0,则x=1,令x=2,则y=1,
中,令y=0,则x=1,令x=2,则y=1,
∴点C(1,0),M(2,1),
∴S=![]() =
=![]() =m-1,
=m-1,
∵3≤m≤5,
∴S的最大值为5-1=4.


科目:初中数学 来源: 题型:
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市是蜜桔之乡,今年桔子大丰收,某合作社要把240吨桔子运往某市的A、B两地,用大、小两种货车共20辆,恰好能一次性运完这批桔子,已知这两种货车的载重量分别为15吨/辆和10吨/辆.
(1)这两种货车各有多少辆?
(2)运往A地的运费为:大车630元/辆,小车420元/辆;运往B地的运费为:大车750元/辆,小车550元/辆.若把20辆货车中的10辆安排前往A地,其余货车前往B地,其中调往A地的大车有a辆,求总运费.(用含a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.

(1)猜想四边形PCOB是什么四边形,并说明理由;
(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(a+3b)、宽为(2a+b)的大长方形;
(1)需要A类、B类和C类卡片的张数分别为( );
A.2,3,7 B.3,7,2
C.2,5,3 D.2,5,7
(2)画出长方形.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
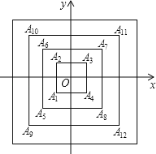
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com