
【题目】如图1,已知抛物线y=x2+mx+m﹣1的顶点为D,交y轴于C点,交x轴于A(x1,0),B(x2,0)两点,点A在y轴左边,点B在y轴右边,且AB=4.
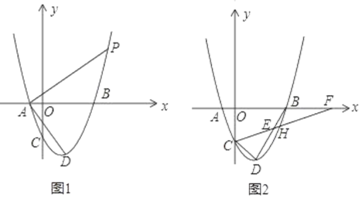
(1)求抛物线的解析式;
(2)如图1,AP⊥AD交抛物线于P.求点P的坐标;
(3)如图2,点H为B,D之间抛物线上一点,直线CH交BD于E,交x轴于F,若S△CDE=S△BEF,求H点的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)P(![]() ,
,![]() );(3)H为(
);(3)H为(![]() ,﹣
,﹣![]() )
)
【解析】
(1)由韦达定理得:x1+x2=-m,x1x2=m-1,而x2-x1=4,即:(x1+x2)2-4x1x2=16,即可求解;
(2)如下图,利用△AEP∽△PFE即可求解;
(3)设直线CF的表达式为y=kx-3求出E、F坐标,利用由S△CDE=S△BEF,即可求解.
解:(1)由韦达定理得:x1+x2=﹣m,x1x2=m﹣1,
而x2﹣x1=4,即:(x1+x2)2﹣4x1x2=16,
解得:m=﹣2,m=6(舍去),
故函数的表达式为:y=x2﹣2x﹣3,
则:A(﹣1,0)、B(3,0)、C(0,﹣3)、D(1,﹣4);
(2)如下图,过A点作y轴的平行线交过P点与x的平行线与E,交过点D与x轴的平行线与F,
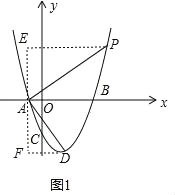
∵AP⊥AD,
∴∠DAF+∠AEP=90°,∠EPA+∠EAP=90°,
∴∠EPA=∠DAF,
∴△AEP∽△PFE,
∴![]() ,
,
设P(m,m2﹣2m﹣3)
其中:PE=m+1,AF=4,AE=m2﹣2m﹣3,FD=2,代入上式,
解得:m=![]() ,m=﹣1(舍去),
,m=﹣1(舍去),
即:P(![]() ,
,![]() );
);
(3)设:直线CF的表达式为y=kx﹣3…①,
直线BD的方程为:y=2x﹣6…②,
联立①、②解得E(![]() ,
,![]() ),F(
),F(![]() ,0),
,0),
过D点做DM∥y轴,交FC于H,

S△CDE=![]() HMxE=
HMxE=![]() (k﹣3+4)
(k﹣3+4)![]() ,
,
S△BEF=![]() BFyE=
BFyE=![]() (
(![]() ﹣3)(
﹣3)(![]() ),
),
由S△CDE=S△BEF,解得:k=2或![]() ,
,
则:CF的表达式为y=2x﹣3或y=![]() x﹣3…③,
x﹣3…③,
将③与二次函数表达式联立,解得:x=![]() 或x=0(舍去),
或x=0(舍去),
故点H为(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】(2016广西贺州市)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某蛋糕店出售网红“奶昔包”,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当以40元每件出售时,每天可以卖300件,当以55元每件出售时,每天可以卖150件.
(1)求y与x之间的函数关系式;
(2)如果规定每天“奶昔包”的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该蛋糕店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试直接写出该“奶昔包”销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:CE=CB.
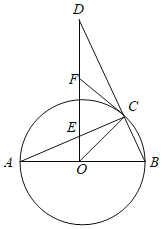
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
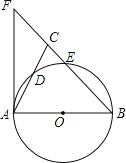
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为S△ABC=36cm2,则梯形EDBC的面积SEDBC为( )
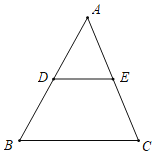
A.9B.18C.27D.30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com