[题目]如图.已知AE=CF.∠AFD=∠CEB.那么添加下列一个条件后.仍无法判定△ADF≌△CBE的是( ) 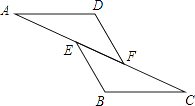A.∠A=∠CB.AD=CBC.BE=DFD.AD∥BC 题目和参考答案——青夏教育精英家教网—

【题目】如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）

A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC

【答案】B
【解析】解：∵AE=CF，
∴AE+EF=CF+EF，
∴AF=CE，
A、∵在△ADF和△CBE中

∴△ADF≌△CBE（ASA），正确，故本选项错误；
B、根据AD=CB，AF=CE，∠AFD=∠CEB不能推出△ADF≌△CBE，错误，故本选项正确；
C、∵在△ADF和△CBE中

∴△ADF≌△CBE（SAS），正确，故本选项错误；
D、∵AD∥BC，
∴∠A=∠C，
∵在△ADF和△CBE中

∴△ADF≌△CBE（ASA），正确，故本选项错误；
故选B．
求出AF=CE，再根据全等三角形的判定定理判断即可．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】根据给出的数轴及已知条件，解答下面的问题：

（1）已知点A，B，C表示的数分别为1，﹣ ，﹣3观察数轴，与点A的距离为3的点表示的数是， B，C两点之间的距离为；
（2）若将数轴折叠，使得A点与C点重合，则与B点重合的点表示的数是；若此数轴上M，N两点之间的距离为2015（M在N的左侧），且当A点与C点重合时，M点与N点也恰好重合，则M，N两点表示的数分别是：M ， N；
（3）若数轴上P，Q两点间的距离为m（P在Q左侧），表示数n的点到P，Q两点的距离相等，则将数轴折叠，使得P点与Q点重合时，P，Q两点表示的数分别为：P ， Q（用含m，n的式子表示这两个数）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】设⊙O的半径为r，P到圆心的距离为d不大于r，则点P在( )

A. 在⊙O内B. 在⊙O外C. 不在⊙O内D. 不在⊙O外

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】(12分)如图，以△ABC的BC边上一点O为圆心的圆，经过A、B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC=FC．

(1)求证：AC是⊙O的切线；

(2)已知圆的半径R=5，EF=3，求DF的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读
（1）阅读理解：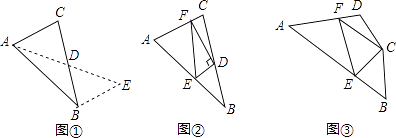

如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．
中线AD的取值范围是；
（2）问题解决：
如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；
（3）问题拓展：
如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．