
【题目】某水果公司以22元/千克的成本价购进1000kg苹果,公司想知道苹果的损坏率,随机抽取若干进行统计,部分结果如下表:
草果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.60 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
根据此表估计这批苹果损坏的概率(精确到0.1),从而计算该公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为_____元/千克.
【答案】50
【解析】
根据利用频率估计概率得到随实验次数的增多,发芽的频率越来越稳定在0.1左右,由此可估计苹果的损坏概率为0.1;根据概率计算出在1000kg苹果中完好苹果的质量为:1000×0.9=900(kg),设每千克苹果的销售价为x元,然后根据“售价=进价+利润”列方程解答.
解:根据表中的损坏的频率,当实验次数增多时,苹果损坏的频率越来越稳定在0.1左右,
所以苹果的损坏概率为0.1.
根据估计的概率可以知道,在1000kg苹果中完好苹果的质量为:1000×0.9=900(kg).
设每千克苹果的销售价为x元,则应有900x=22×1000+23000,
解得x=50.
答:出售苹果时每千克大约定价为50元可获利润23000元.
故答案为:50.


科目:初中数学 来源: 题型:
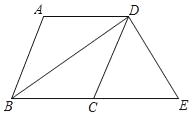
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
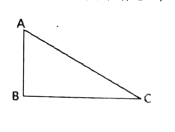
【题目】如图,在![]() 中,
中,![]() .
.
(1)作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ;(要求:不写作法,保留作图痕迹)
;(要求:不写作法,保留作图痕迹)
(2)判断(1)中![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
(3)若![]() ,求出(1)中
,求出(1)中![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
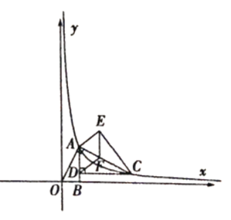
【题目】已知:如图,![]() 的顶点
的顶点![]() 是反比例函数
是反比例函数![]() 图象上一点,过点
图象上一点,过点![]() 作
作![]() 交反比例函数的图象于点
交反比例函数的图象于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
(1)求点![]() 的坐标;
的坐标;
(2)将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,连接
,连接![]() ,判断四边形
,判断四边形![]() 的形状并说明理由.
的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班要从甲乙两名同学中选派一人去参加学校举行的”扫黑除恶”知识竞赛,王老师准备用一副扑克牌中排列数字分别为![]() ,
,![]() ,
,![]() ,
,![]() 的四张扑克牌做抽数字游戏,决定谁去参加比赛,游戏规则为;将这四张牌的正面全部朝下,洗匀后从中随机抽取一张,得到的数字作为十位上的数字,然后将所抽到的牌放回,再从中随机抽取一张,得到的数字作为个位上的数字,这样就得到了一个两位数,若这个两位数小于
的四张扑克牌做抽数字游戏,决定谁去参加比赛,游戏规则为;将这四张牌的正面全部朝下,洗匀后从中随机抽取一张,得到的数字作为十位上的数字,然后将所抽到的牌放回,再从中随机抽取一张,得到的数字作为个位上的数字,这样就得到了一个两位数,若这个两位数小于![]() ,则甲胜,否则乙获胜,且游戏的获胜者将去参加比赛.
,则甲胜,否则乙获胜,且游戏的获胜者将去参加比赛.
(1)求抽取的扑克牌使得十位数字是![]() 的概率;
的概率;
(2)你认为这个游戏公平吗?请运用概率知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
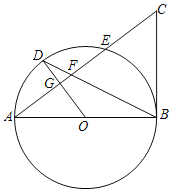
【题目】如图所示,AB是⊙O的直径,G为弦AE的中点,OG的延长线交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为10,tanA=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
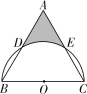
【题目】如图,等边△ABC的边长为4,以BC为直径的半圆O交AB于点D,交AC于点E,则图中阴影部分的面积是( )
A.2![]() -
-![]() B.2
B.2![]() -
-![]()
C.4![]() +-
+-![]() D.4
D.4![]() -
-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com