
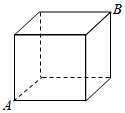
 如图,一只昆虫在棱长为20cm的正方体的表面上爬行,则它从图中的顶点A爬到顶点B的最短距离为( )
如图,一只昆虫在棱长为20cm的正方体的表面上爬行,则它从图中的顶点A爬到顶点B的最短距离为( )| A. | 40cm | B. | 60cm | C. | $20\sqrt{5}cm$ | D. | $40\sqrt{3}cm$ |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
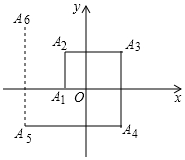 如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为(-2008,-2006),.
如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为(-2008,-2006),.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 14 | 15 | 23 | 16 | 20 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
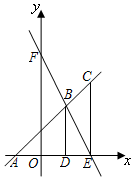 如图,在直角坐标系中,点C在直线AB上,点A、B的坐标分别是(-1,0),(1,2),点C的横坐标为2,过点B作BD⊥x轴于D,过点C作CE⊥x轴于E,直线BE与y轴交于点F.
如图,在直角坐标系中,点C在直线AB上,点A、B的坐标分别是(-1,0),(1,2),点C的横坐标为2,过点B作BD⊥x轴于D,过点C作CE⊥x轴于E,直线BE与y轴交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
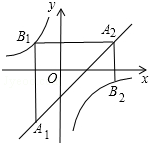 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在反比例函数y=-$\frac{1}{x}$的图象上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2017=-1.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在反比例函数y=-$\frac{1}{x}$的图象上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2017=-1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-2)2-1 | B. | y=(x-2)2+1 | C. | y=(X+2)2+1 | D. | y=(x+2)2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com