
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,先移动到
点出发,先移动到![]() 轴上的点
轴上的点![]() 处,再沿垂直于
处,再沿垂直于![]() 轴的方向向左移动1个单位至点
轴的方向向左移动1个单位至点![]() 处,最后移动到点
处,最后移动到点![]() 处停止.当点
处停止.当点![]() 移动的路径最短时 (即三条线段
移动的路径最短时 (即三条线段![]() 、
、![]() 、
、![]() 长度之和最小),点
长度之和最小),点![]() 的坐标为( )
的坐标为( )
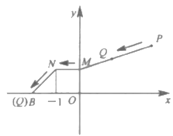
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
将BN向右平移1个单位得到AM,连接AB,可得四边形ABNM是平行四边形,当A,M,P在同一直线上时,AM+PM有最小值,即为线段AP的长,因此BN+PM的最小值为AP长,此时PM、MN、NB长度之和最小,通过求直线AP的解析式,即可得到点M的坐标.
解:如图,将BN向右平移1个单位得到AM,连接AB,则BN=AM,
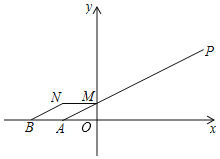
易得,四边形ABNM是平行四边形,
∴MN=AB=1,
∴当A,M,P在同一直线上时,AM+PM有最小值,最小值为线段AP的长,
因此BN+PM的最小值也为AP长,
此时PM、MN、NB长度之和最小,
∵P(3,2),B(-2,0),AB=1,
∴A(-1,0),
设直线AP的解析式为y=kx+b,将P(3,2),A(-1,0)代入得,
![]() ,
,
解得![]() ,
,
∴直线AP解析式为![]() ,
,
当x=0时,![]() ,即M点坐标为(0,
,即M点坐标为(0,![]() ),
),
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 的中点,过点
的中点,过点![]() 的射线
的射线![]() 与
与![]() 成
成![]() 的角,点
的角,点![]() 为射线
为射线![]() 上一动点,给出以下四个结论:
上一动点,给出以下四个结论:
①当![]() ,垂足为
,垂足为![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③在射线![]() 上,使
上,使![]() 为直角三角形的点
为直角三角形的点![]() 只有1个;
只有1个;
④在射线![]() 上,使
上,使![]() 为等腰三角形的点
为等腰三角形的点![]() 只有1个;
只有1个;
其中正确结论的序号是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是△ABC中∠A、∠B、∠C的对边,抛物线y=x2﹣2ax+b2交x轴于M(a+c,0),则△ABC是( )
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3
(1)请你把已知的二次函数化成y=(x﹣h)2+k的形式,并在平面直角坐标系中画出它的图象;
(2)如果A(x1,y1)、B(x2,y2)是(1)中像上的两点,且x1<x2<1,请直接写出y1、y2的大小关系为 .
(3)利用(1)中的图象表示出方程x2﹣2x﹣1=0的根,画在(1)的图象上即可,要求保留画图痕迹.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 、
、![]() 两个圆柱形容器放置在同一水平桌面上,开始时容器
两个圆柱形容器放置在同一水平桌面上,开始时容器![]() 中盛满水,容器
中盛满水,容器![]() 中盛有高度为1 dm的水,容器
中盛有高度为1 dm的水,容器![]() 下方装有一只水龙头,容器
下方装有一只水龙头,容器![]() 向容器
向容器![]() 匀速注水.设时间为t (s),容器
匀速注水.设时间为t (s),容器![]() 、
、![]() 中的水位高度
中的水位高度![]() (dm)、
(dm)、![]() (dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
(dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
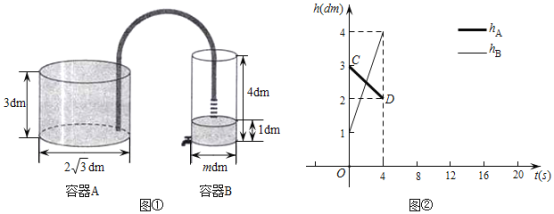
(1)容器![]() 向容器
向容器![]() 注水的速度为 dm3/s(结果保留
注水的速度为 dm3/s(结果保留![]() ),容器
),容器![]() 的底面直径
的底面直径![]() dm;
dm;
(2)当容器![]() 注满水后,容器
注满水后,容器![]() 停止向容器
停止向容器![]() 注水,同时开启容器
注水,同时开启容器![]() 的水龙头进行放水,放水速度为
的水龙头进行放水,放水速度为![]() dm3/s.请在图②中画出容器
dm3/s.请在图②中画出容器![]() 中水位高度
中水位高度![]() 与时间 (
与时间 (![]() )的函数图像,说明理由;
)的函数图像,说明理由;
(3)当容器B注满水后,容器A继向容器B注水,同时开启容器B的水龙头进行放水,放水速度为![]() dm3/s,直至容器
dm3/s,直至容器![]() 、
、![]() 水位高度相同时,立即停止放水和注水,求容器
水位高度相同时,立即停止放水和注水,求容器![]() 向容器
向容器![]() 全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.
,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿
沿![]() 折叠压平,使点
折叠压平,使点![]() 落在坐标平面内,设点
落在坐标平面内,设点![]() 的对应点为点
的对应点为点![]() .若抛物线
.若抛物线![]() (
(![]() 且
且![]() 为常数)的顶点落在
为常数)的顶点落在![]() 的内部,则
的内部,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com