
分析 由x2+x-1=0得到x2=-(x-1),将$\frac{{x}^{4}+(x-1)^{2}-1}{x(x-1)}$变形为$\frac{2(x-1)^{2}-1}{x(x-1)}$,进一步得到原式=$\frac{2{x}^{2}-4x+1}{{x}^{2}+x-2x}$=$\frac{2(1-x)-4x+1}{1-2x}$,再化简后约分计算即可求解.
解答 解:∵x2+x-1=0
∴x2=-(x-1),
∴$\frac{{x}^{4}+(x-1)^{2}-1}{x(x-1)}$
=$\frac{2(x-1)^{2}-1}{x(x-1)}$
=$\frac{2{x}^{2}-4x+1}{{x}^{2}+x-2x}$
=$\frac{2(1-x)-4x+1}{1-2x}$
=$\frac{3(1-2x)}{1-2x}$
=3.
故答案为:3.
点评 考查了分式的值,分式求值历来是各级考试中出现频率较高的题型,而条件分式求值是较难的一种题型,在解答时应从已知条件和所求问题的特点出发,通过适当的变形、转化,才能发现解题的捷径.


科目:初中数学 来源: 题型:解答题
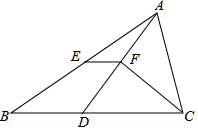 如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
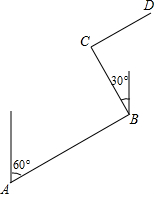 幸福乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东60°的方向到B村,从B村沿北偏西30°方向到C村.若水渠从C村沿CD方向修建可以保持与AB的方向一致,则∠DCB的度数为90°.
幸福乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东60°的方向到B村,从B村沿北偏西30°方向到C村.若水渠从C村沿CD方向修建可以保持与AB的方向一致,则∠DCB的度数为90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
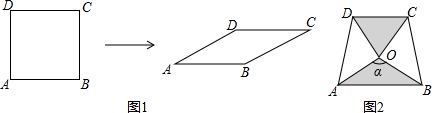
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com