
如图所示,已知线段AB,点C是AB的黄金分割点,且AC>BC,点D在AB上,且满足BD2=AD·AB,请说明点C、D分别是线段BD、AC的黄金分割点.
|
解答:因为C是AB的黄金分割点,且AC>BC,所以 又因为BD2=AD·AB,即 根据黄金分割点的定义,可知D也是AB的黄金分割点,且BD>AD, 所以 由①,②两式可知AC=BD= 则 所以点D是线段AC的黄金分割点,且AD>DC 同理点C是线段BD的黄金分割点,且BC>CD. 分析:已知线段AB及AB上一点C,若想判断C是否为AB的黄金分割点,可按下面两种方法进行:(1)分别算出AC与全线段AB,CB与AC的比,如果比值相同,那么C是AB的黄金分割点,否则不是.(2)算出其中一组比的比值,如果等于 |
|
注意:一条线段上有两个黄金分割点,所以说黄金分割点时要强调两条线段的大小. |


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
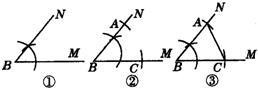
查看答案和解析>>
科目:初中数学 来源: 题型:
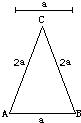 5、如图所示,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.
5、如图所示,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com